Daha önce burada Cooley-Tukey FFT algoritması ile ilgili bir yazı yazmıştım. Bu yazımda ise bu algoritmayı kullanarak FPGA üzerinde hızlı fourier dönüşümü işlemi yapacağım.
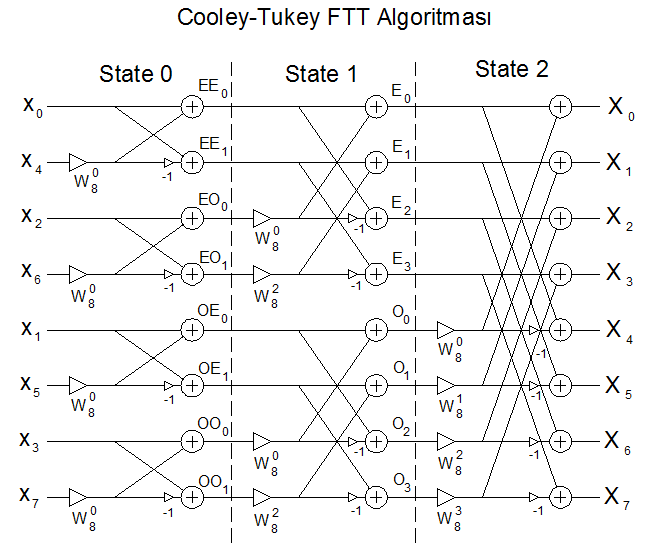
için Cooley-Tukey FFT algoritmasının şematik gösterimim şu şekildedir:
Buradaki en küçük parça Butterfly olarak adlandırılır:
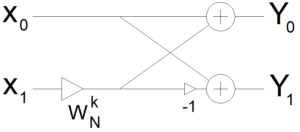Burada 
Twiddle Factor'dür ve şu şekilde tanımlanır:
Buradaki sinüs ve kosinüs değerleri FPGA üzerinde bir tabloda tutulabilir(look-up table) ya da CORDIC gibi bir algoritma ile hesaplanabilir. Bu uygulamada sinüs ve kosinüs değerleri bir tabloda tutulacaktır.
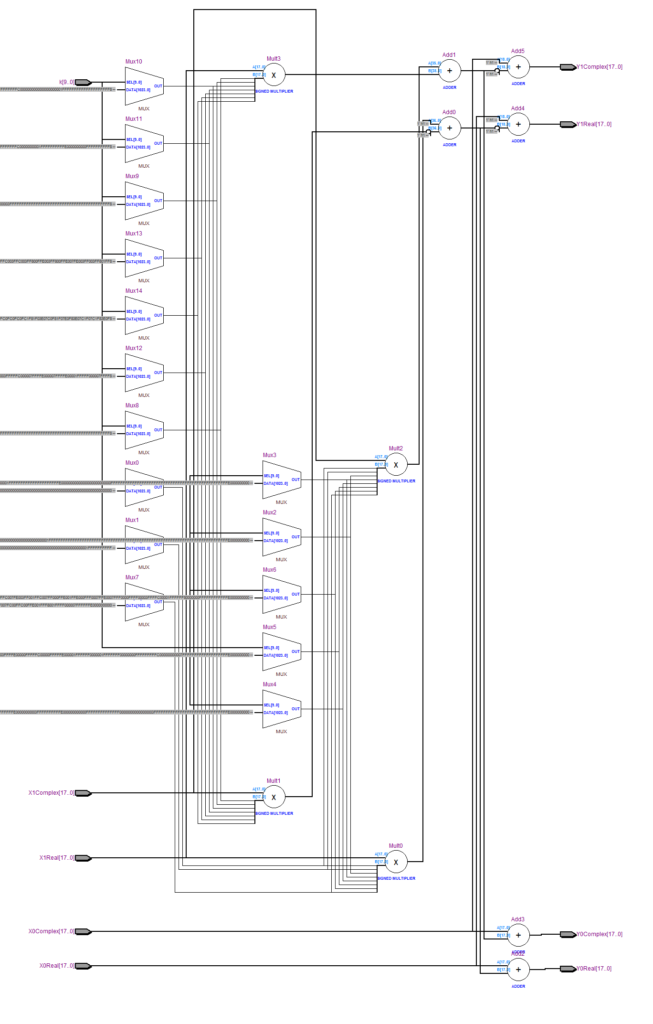
Butterfly modülünün VHDL kodu:
---------------------------------------------------------- -- CFFT_Radix2_Butterfly.vhd -- Bertan Taşkın -- 1.6.2017 -- -- 2 noktalı Complex Fast Fourier Dönüşümü gerçekleştiren modül. -- FFT işlemindeki toplam nokta sayısı generic kısmındaki -- FFT_Power ile belirlenir. Sinüs ve Kosinüs tabloları -- bu değere göre hesaplanır. Giriş verisinin genişliği -- generic kısmındaki Data_Width ile belirlenir. FFT işlemi -- fixed-point sayılar üzerinde gerçekleştiğinde dolayı -- işlem hassasiyetini arttırmak için veri genişliğine -- FFT_Power'da eklenir. -- -- Veri giriş ve çıkışları real ve complex olmak üzere -- toplamda 8 sinyal üzerinden gerçekleşir. Twiddle -- factor kuvveti k sinyali üzerinden gönderilir. Modül -- asenkron çalışarak çıkış verilerini üretir. -- -- Modülün doğru çalışabilmesi için Data_Width değeri, integer -- genişliği olan 32'den büyük olmamalıdır! -- -- Sinüs ve Kosinüs değerleri önceden hesaplanmış tablolarda -- saklandığından dolayı modülün FPGA üzerinde harcadığı -- toplam LE sayısı yaklaşık olarak, Data_Width değeri ile -- doğru orantılı, FFT_Power ile karesel orantılıdır. -- -- Modülün yaklaşık max. çalışmak frekansı gömülü çarpıcı -- elemanların hızı kadardır. -- ---------------------------------------------------------- --Kütüphaneler library IEEE; use IEEE.STD_LOGIC_1164.ALL; USE ieee.numeric_std.ALL; use ieee.math_real.all; entity CFFT_Radix2_Butterfly is generic(Data_Width : integer := 6; --İşlenecek verinin boyutu FFT_Power : integer := 3); --Hesaplanacak FFT Kuvveti port(k : in std_logic_vector(FFT_Power - 2 downto 0); --Twiddle Factor kuvveti (Wk) X0Real, X0Complex : in std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Girişi - 0 X1Real, X1Complex : in std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Girişi - 1 Y0Real, Y0Complex : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Cıkışı - 0 Y1Real, Y1Complex : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0)); --Complex ve Real Veri Cıkışı - 1 end CFFT_Radix2_Butterfly; architecture Behavioral of CFFT_Radix2_Butterfly is --Table veri tipi oluşturuluyor type Table is array(2**(FFT_Power - 1) - 1 downto 0) of signed(Data_Width + FFT_Power - 1 downto 0); signal SinTable, CosTable : Table; signal X0RealS, X0ComplexS, X1RealS, X1ComplexS : signed(Data_Width + FFT_Power - 1 downto 0); signal Y0RealS, Y0ComplexS, Y1RealS, Y1ComplexS : signed(Data_Width + FFT_Power - 1 downto 0); signal X1RealW, X1ComplexW : signed(Data_Width + FFT_Power - 1 downto 0); signal kint : integer; begin --Twiddle Factor kuvveti integer'a dönüştürülüyor kint <= to_integer(unsigned(k)); --Giriş verileri işlem kolaylığı için signed tipine dönüştürülüyor X0RealS <= signed(X0Real); X0ComplexS <= signed(X0Complex); X1RealS <= signed(X1Real); X1ComplexS <= signed(X1Complex); --Sinüs Tablosu / sin(-2*pi*i/N) Sine : for i in 0 to 2**(FFT_Power - 1) - 1 generate constant SinReal : REAL := SIN(real(-2) * MATH_PI * real(i) / real(2**FFT_Power)); begin SinTable(i) <= to_signed(integer(SinReal * real(2**(Data_Width - 1))), Data_Width + FFT_Power); end generate; --Kosinüs Tablosu / cos(-2*pi*i/N) Cosine : for i in 0 to 2**(FFT_Power - 1) - 1 generate constant CosReal : REAL := COS(real(-2) * MATH_PI * real(i) / real(2**FFT_Power)); begin CosTable(i) <= to_signed(integer(CosReal * real(2**(Data_Width - 1))), Data_Width + FFT_Power); end generate; ----------FFT işlemleri---------- --Değişkenlerin açıklaması: --X0R : 0. giriş verisinin reel kısmı --X0C : 0. giriş verisinin complex kısmı --X1R : 1. giriş verisinin reel kısmı --X1C : 1. giriş verisinin complex kısmı --Y0R : 0. cıkış verisinin reel kısmı --Y0C : 0. cıkış verisinin complex kısmı --Y1R : 1. cıkış verisinin reel kısmı --Y1C : 1. cıkış verisinin complex kısmı --X1RW : 1. giriş verisinin Twiddle factor ile çarpılmış halinin reel kısmı --X1CW : 1. giriş verisinin Twiddle factor ile çarpılmış halinin complex --FFT işlemi: --Y0 = X0 + X1 * W_k --Y1 = X0 - X1 * W_k --Twiddle factor: --W_k = cos(k) + i*sin(k) --Complex çarpma işlemi: --(a+bi)*(c+di) = (ac - bd)+i(ad+bc) --X1RW = X1R * cos(k) - X1C * sin(k) --X1CW = X1C * cos(k) + X1R * sin(k) --Çarpma işlemi sonucunda çıkan sonuç Data_Width kadar sağa kaydırılır X1RealW <= shift_right(signed(X1RealS * CosTable(kint) - X1ComplexS * SinTable(kint)), Data_Width - 1)(Data_Width + FFT_Power - 1 downto 0); X1ComplexW <= shift_right(signed(X1ComplexS * CosTable(kint) + X1RealS * SinTable(kint)), Data_Width - 1)(Data_Width + FFT_Power - 1 downto 0); --Y0R = X0R + X1RW --Y0C = X0C + X1CW Y0RealS <= X0RealS + X1RealW; Y0ComplexS <= X0ComplexS + X1ComplexW; --Y1R = X0R - X1RW --Y1C = X0C - X1CW Y1RealS <= X0RealS - X1RealW; Y1ComplexS <= X0ComplexS - X1ComplexW; --------------------------------- --Çıkış değerleri tekrar eski haline(std_logic_vector) döndürülüyor Y0Real <= std_logic_vector(Y0RealS); Y0Complex <= std_logic_vector(Y0ComplexS); Y1Real <= std_logic_vector(Y1RealS); Y1Complex <= std_logic_vector(Y1ComplexS); end Behavioral;
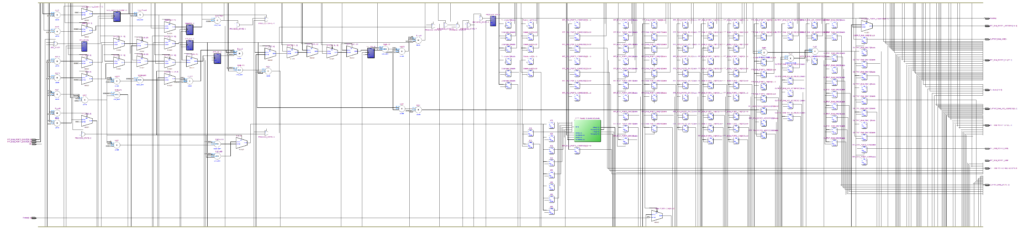
Quartus II ile oluşturulmuş RTL şeması:
FFT işlemi 2 adımda gerçekleşir; Yeni verilerin alınması, FFT hesabı.
1.Yeni verilerin alınması
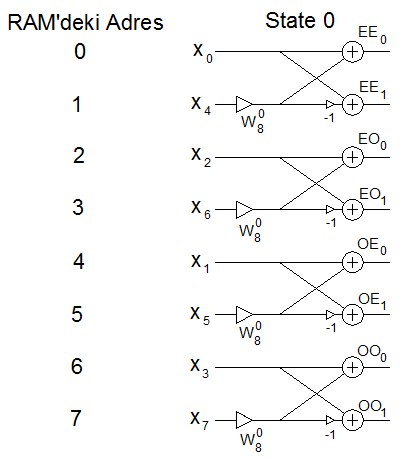
Cooley-Tukey algoritmasında yukarıda da görüldüğü gibi giriş verilerinin işlem sırası için sırasıyla 
şeklindedir. FFT hesabının daha kolay yapılabilmesi için giriş verileri bu sıra ile RAM'e yazılması gerekir. Bu sırayı elde etmek için !!Bit-Reversal Permutation algoritması kullanılır. Bu algoritmaya göre giriş verisinin sırasının bitlerini ters çevirirsek verinin yazılacağı RAM adresini buluruz. Örnek olarak 
giriş verisinin RAM'de yazılacağı adres 
'dır. Bu işlem sonunda veriler RAM'de aşağıdaki sıra ile dizilmiş olacaktır.
2.FFT Hesabı
FFT hesabı 2 adımda gerçekleşir; RAM'den eski verilerin okunması, RAM'e yeni verilerin yazılması
2.1. RAM'den Eski Verilerin Okunması
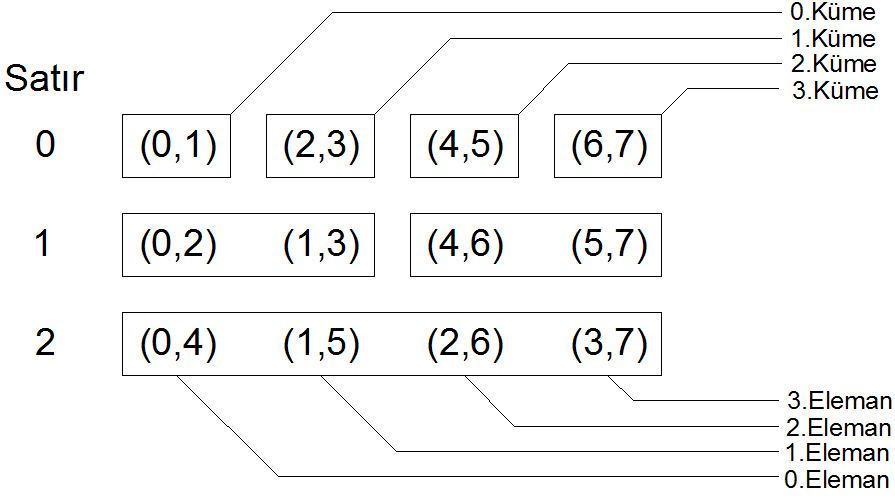
FFT hesabının doğru gerçekleşmesi için RAM'den veriler doğru sıra ile okunmalıdır. için Butterfly'a girecek verilerin RAM'deki sırası sırasıyla 
şeklindedir. Bu sayı gruplarını Satır, Küme ve Eleman şeklinde düzenlersek RAM'den verilerin hangi sıra ile okunacağını daha kolay anlayabiliriz.
Bu şemaya göre RAM'den okunacak verilerin sırası hakkında şu kuralları söyleyebiliriz:
FFT kuvveti(
) olmak üzere toplam satır sayısı 'dir.
satırdaki toplam küme sayısı ise 
'dir.- satırdaki bir kümenin içindeki toplam eleman sayısı ise
'dir. - satırdaki her bir kümenin ilk elemanının
değeri, o kümenin index sayısının 
katıdır. - Herhangi bir kümedeki bir sonraki elemanın ve
değerleri, bir önceki elemanın ve değerlerinden 
fazladır. - satırdaki bir elemanın ve değerleri arasındaki fark
'dir. - satırdaki twidle factor kuvveti, elemanın index sayısının katıdır.
2.1. RAM'e yeni verlerin yazılması
RAM'e yazılan veriler, okunan veriler ile aynı adreste olacaktır. En son satırda hesaplanan sonuçların magnitude karesi alınıp aynı anda çıkış verilerinin tutulacağı RAM'e de yazılacaktır. Çıkış verilerinin farklı RAM'de tutulması ile yeni FFT işlemi yapılırken eski sonuçların da erişimi sağlanır.
Tasarımın VHDL kodu:
----------------------------------------------------------
-- CFFT_Engine.vhd
-- Bertan Taşkın
-- 1.6.2017
--
-- Complex Hızlı Fourier Dönüşümü Alan Modül.
-- FFT işlemindeki toplam nokta sayısı generic kısmındaki
-- FFT_Power ile belirlenir. Giriş verisinin genişliği Data_Width
-- ile belirlenir. FFT işlemi fixed-point sayılar üzerinden
-- yapıldığından dolayı hassasiyeti arttırmak için veri genişliğine
-- FFT_Power'da eklenmiştir. Modül yüksek hızlı Clock sinyali ile
-- çalıştığından dolayı DataIn sinyalinden okunan verilerin hızını
-- yavaşlatmak için ADC_Sampling_Cycle değişkeni eklenmiştir.
--
-- FFT_RAM, FFT işlemi alınırken kullanılan RAM'dir. Dual-Port
-- yapıdadır. RAM'in çıkış sinyalleri(q_a, q_b) asenkron yapıda olmak
-- zorundadır. Her bir port 2*(Data_Width+FFT_Power) bit genişliğinde
-- olmalıdır. Kapasitesi ise 2*2^FFT_Power*(Data_Width+FFT_Power)Bit
-- olmalıdır.
--
-- OUTPUT_RAM, FFT işlemi sonucunda çıkan sonuçların tutulduğu RAM'dir.
-- SemiDual-Port yada Dual-Port yapıda olabilir. Giriş portu
-- Data_Width+FFT_Power bit olmalıdır. Kapasitesi ise
-- 2^(FFT_Power-1)(Data_Width+FFT_Power) olmalıdır.
--
-- ADC verilerinin alınma işlemi toplamda ADC_Sampling_Cycle*2^FFT_Power
-- cycle'da gerçekleşir.
--
-- FFT işlemi için gereken cycle 2*2^(FFT_Power-1)*FFT_Power şeklinde
-- hesaplanır.
--
-- FFT sonuçları magnitude değildir, magnitude karedir.
--
-- Data_Width'in alabileceği en büyük değer integer genişliği
-- olan 32'dir.
--
----------------------------------------------------------
--Kütüphaneler
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
USE ieee.numeric_std.ALL;
use ieee.math_real.all;
entity CFFT_Engine is
generic(FFT_Power : integer := 3; --FFT Kuvveti
Data_Width : integer := 8; --İşlenecek Verinin Boyutu
Sampling_Cycle : integer := 250); --ADC İçin Sampling Cycle Süresi
--FFT İçin Örnekleme Frekansı = Clk / Sampling_Cycle
port(Clk : in std_logic; --Clock Girşi
DataIn : in std_logic_vector(Data_Width - 1 downto 0); --ADC Veri Giriş Sinyali
Reading : out std_logic; --ADC Okuması Yapılıp Yapılmadığını Belirten Sinyal
DataIndex : out std_logic_vector(FFT_Power - 1 downto 0); --O Anki Okunan ADC Verisinin Sırası
--FFT Hesaplmalarında Kullanılacak RAM'in Sinyalleri
FFT_RAM_PORT1_DIN, FFT_RAM_PORT2_DIN : out std_logic_vector((Data_Width + FFT_Power) * 2 - 1 downto 0); --Veri Giriş Sinyalleri
FFT_RAM_PORT1_DOUT, FFT_RAM_PORT2_DOUT : in std_logic_vector((Data_Width + FFT_Power) * 2 - 1 downto 0); --Veri Çıkış Sinyalleri
FFT_RAM_PORT1_ADDRESS, FFT_RAM_PORT2_ADDRESS : out std_logic_vector(FFT_Power - 1 downto 0); --Adres Sinyalleri
FFT_RAM_PORT1_WRE, FFT_RAM_PORT2_WRE : out std_logic; --Yazma Aktif Sinyalleri
--Çıkış Verilerinin Tutulacağı RAM'in Sinyalleri
OUTPUT_RAM_DIN : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Veri Giriş Sinyali
OUTPUT_RAM_WR_ADDRESS : out std_logic_vector(FFT_Power - 2 downto 0); --Adres Sinyali
OUTPUT_RAM_WREN : out std_logic); --Yazma Aktif Sinyali
end CFFT_Engine;
architecture Behavioral of CFFT_Engine is
--Girilen verinin bitlerini ters çeviren fonksiyon
--ADC den alınan verilerin sırası bu fonksiyon ile belirlenir
function Reverse_Bit(Data : std_logic_vector) return std_logic_vector is
variable X : std_logic_vector(Data'length - 1 downto 0) := (others => '0');
begin
a : for i in 0 to Data'length - 1 loop
X(i) := Data(Data'length - 1 - i);
end loop;
return X;
end Reverse_Bit;
--Girilen veriyi işaret bitine dikkat ederek yeniden boyutlandıran fonksiyon
function Resize_Bit(Data : std_logic_vector; NewSize : integer) return std_logic_vector is
variable X : std_logic_vector(NewSize - 1 downto 0) := (others => '0');
begin
--Data verisinin işaret biti hariç diğer bitleri X değikenine aktarılır
a : for i in 0 to Data'length - 2 loop
X(i) := Data(i);
end loop;
--X değişkeninde kalan bitler Data verisinin işaret biti ile doldurulur
b : for i in Data'length - 1 to NewSize - 1 loop
X(i) := Data(Data'length - 1);
end loop;
return X;
end Resize_Bit;
--FFT işlemini gerçekleştirecek Butterfly komponenti
component CFFT_Radix2_Butterfly
generic(Data_Width : integer := 6; --İşlenecek verinin boyutu
FFT_Power : integer := 3); --Hesaplanacak FFT Kuvveti
port(k : in std_logic_vector(FFT_Power - 2 downto 0); --Twiddle Factor kuvveti (Wk)
X0Real, X0Complex : in std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Girişi - 0
X1Real, X1Complex : in std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Girişi - 1
Y0Real, Y0Complex : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Complex ve Real Veri Cıkışı - 0
Y1Real, Y1Complex : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0)); --Complex ve Real Veri Cıkışı - 1
end component;
signal k : std_logic_vector(FFT_Power - 2 downto 0);
signal Enable : std_logic;
signal X0Real, X0Complex, X1Real, X1Complex : std_logic_vector(Data_Width + FFT_Power - 1 downto 0);
signal Y0Real, Y0Complex, Y1Real, Y1Complex : std_logic_vector(Data_Width + FFT_Power - 1 downto 0);
type PROCESS_STATE_TYPE is (SAMPLING_ADC_DATA, CALCULATE_FFT);
type FFT_STATE_TYPE is (READ_RAM, WRITE_RAM);
signal Re, Im : signed((Data_Width + FFT_Power) - 1 downto 0);
signal MagnitudeSquare : unsigned((Data_Width + FFT_Power) * 2 - 1 downto 0);
begin
--FFT işlemini gerçekleştirecek Butterfly komponentinin üretilmesi
UButterfly : CFFT_Radix2_Butterfly
generic map(Data_Width, FFT_Power)
port map(k,
X0Real, X0Complex, X1Real, X1Complex,
Y0Real, Y0Complex, Y1Real, Y1Complex);
--FFT_RAM'in çıkış sinyalleri Butterfly'a bağlanır
--Butterfly'ın çıkış sinyallerinden de FFT sonucu alınır
X0Real <= FFT_RAM_PORT1_DOUT((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power));
X0Complex <= FFT_RAM_PORT1_DOUT((Data_Width + FFT_Power) - 1 downto 0);
X1Real <= FFT_RAM_PORT2_DOUT((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power));
X1Complex <= FFT_RAM_PORT2_DOUT((Data_Width + FFT_Power) - 1 downto 0);
--Butterfly'ın Y0 çıkışındaki verinin magnitude karesi hesaplanır
--(Magnitude değil!)
Re <= signed(Y0Real);
Im <= signed(Y0Complex);
MagnitudeSquare <= unsigned((Re*Re)+(Im*Im));
--ADC'den veri alma ve FFT işleminin organizasyonunu sağlayan process
process(Clk)
variable State0 : integer range 0 to 2**FFT_Power - 1 := 0;
variable FFT_S : integer range 0 to FFT_Power - 1 := 0;
variable FFT_K, FFT_E : integer range 0 to 2**(FFT_Power - 1) - 1 := 0;
variable PROCESS_STATE : PROCESS_STATE_TYPE := SAMPLING_ADC_DATA;
variable FFT_STATE : FFT_STATE_TYPE := READ_RAM;
variable ADC_Sampling_Cycle : integer range 0 to Sampling_Cycle - 1 := 0;
begin
--ADC'den verilerin alınması
if PROCESS_STATE = SAMPLING_ADC_DATA then
--Okuma yapıldığı için Reading sinyali setlenir
Reading <= '1';
--O an okunan ADC verisinin sırası
DataIndex <= std_logic_vector(to_unsigned(State0, FFT_Power));
--Okunan veriler, veri sırasının bitlerinin yerlerinin değiştirilmesiyle oluşan adrese yazılır
FFT_RAM_PORT1_ADDRESS <= Reverse_Bit(std_logic_vector(to_unsigned(State0, FFT_Power)));
--ADC den alınan veriler FFT_RAM'in DIN sinyaline gönderilir
--Reel kısım = ADC verisi, Complex kısım = 0
FFT_RAM_PORT1_DIN((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power)) <= std_logic_vector(Resize_Bit(DataIn, Data_Width + FFT_Power));--std_logic_vector(resize(signed(DataIn), Data_Width + FFT_Power));
FFT_RAM_PORT1_DIN((Data_Width + FFT_Power) - 1 downto 0) <= (others=>'0');
--Sadece PORT1 den yazma işlemi yapılacağından PORT1_WRE setlenir
FFT_RAM_PORT1_WRE <= '1';
FFT_RAM_PORT2_WRE <= '0';
OUTPUT_RAM_WREN <= '0';
--FFT işleminin yapılması
elsif PROCESS_STATE = CALCULATE_FFT then
--Okuma yapılmadığı için Reading resetlenir
Reading <= '0';
--Twiddle factor
k <= std_logic_vector(to_unsigned(FFT_E * (2**(FFT_Power - FFT_S - 1)), FFT_Power - 1));
--Kullanılacak Adres
FFT_RAM_PORT1_ADDRESS <= std_logic_vector(to_unsigned(FFT_K * (2**(FFT_S + 1)) + FFT_E, FFT_Power));
FFT_RAM_PORT2_ADDRESS <= std_logic_vector(to_unsigned(FFT_K * (2**(FFT_S + 1)) + (2**FFT_S) + FFT_E, FFT_Power));
OUTPUT_RAM_WR_ADDRESS <= std_logic_vector(to_unsigned(FFT_E, FFT_Power - 1));
--Eğer FFT işleminin son satırında ise çıkan sonuçlar OUTPUT_RAM'e de yazılır
if FFT_S = (FFT_Power - 1) then
OUTPUT_RAM_WREN <= '1';
else
OUTPUT_RAM_WREN <= '0';
end if;
--Butterfly'dan çıkan veriler tekrar FFT_RAM'e yazılır
FFT_RAM_PORT1_DIN((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power)) <= Y0Real;
FFT_RAM_PORT1_DIN((Data_Width + FFT_Power) - 1 downto 0) <= Y0Complex;
FFT_RAM_PORT2_DIN((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power)) <= Y1Real;
FFT_RAM_PORT2_DIN((Data_Width + FFT_Power) - 1 downto 0) <= Y1Complex;
--Aynı anda Butterfly'dan çıkan verilerden magnitude square hesaplanır ve OUTPUT_RAM'in
--veri giriş sinyalne aktarılır.
--OUTPUT_RAM'in WRE sinyali setlenmeden bu veri OUTPUT_RAM'e yazılmaz
OUTPUT_RAM_DIN <= std_logic_vector(MagnitudeSquare((Data_Width + FFT_Power) * 2 - 1 downto (Data_Width + FFT_Power)));
--FFT hesaplaması 2 cycle'da gerçekleşir
--1.Cycle FFT_RAM'den eski veriler okunur
--Bu cycle'da yazma yapılmayacağından dolayı WRE sinyali resetlenir
if FFT_STATE = READ_RAM then
FFT_RAM_PORT1_WRE <= '0';
FFT_RAM_PORT2_WRE <= '0';
--2.Cycle'da Butterfly'dan çıkan yeni veriler FFT_RAM'e yazılır
--Yazma yapılacağından dolayı WRE sinyal setlenir
elsif FFT_STATE = WRITE_RAM then
FFT_RAM_PORT1_WRE <= '1';
FFT_RAM_PORT2_WRE <= '1';
end if;
end if;
--Yukarıdaki işlemlerde kullanılan değişkenler Clk sinyalinin
--yükselen kenarı ile güncellenir
if rising_edge(Clk) then
--ADC verilerinin örneklenmesi
if PROCESS_STATE = SAMPLING_ADC_DATA then
--Sampling_Cycle kadar beklenir
if ADC_Sampling_Cycle < Sampling_Cycle - 1 then
ADC_Sampling_Cycle := ADC_Sampling_Cycle + 1;
else
ADC_Sampling_Cycle := 0;
--Sampling_Cycle'a ulaşıldığında State0 değişkeni 1 arttırılır
--ve bir sonraki ADC verisi için Sampling_Cycle saymaya başlanır
if State0 < 2**FFT_Power - 1 then
State0 := State0 + 1;
else
--Bütün ADC verilerinin örneklemesi bitince FFT hesaplama adımına geçilir
State0 := 0;
PROCESS_STATE := CALCULATE_FFT;
end if;
end if;
--FFT işlemlerinin hesaplanması
elsif PROCESS_STATE = CALCULATE_FFT then
--FFT_RAM'den veriler okunduktan sonra yazma işlemine geçilir
if FFT_STATE = READ_RAM then
FFT_STATE := WRITE_RAM;
--Yazma işleminden sonra tekrar okuma işlemine geçilir
elsif FFT_STATE = WRITE_RAM then
FFT_STATE := READ_RAM;
--FFT hesabında kullanılan değişkenlerin güncellenmesi
--FFT_S: Satır indexi
--FFT_K: Küme indexi
--FFT_E: Eleman indexi
--Eleman sonuna ulaşıldı ise
if FFT_E = 2**FFT_S - 1 then
--Küme sonuna da ulaşıldı ise
if FFT_K = 2**(FFT_Power - FFT_S - 1) - 1 then
--Satır sonuna da ulaşıldı ise
if FFT_S = FFT_Power - 1 then
--FFT işlemi bitmiştir
--Başa dön ve ADC verilerini tekrar örnekle
PROCESS_STATE := SAMPLING_ADC_DATA;
FFT_S := 0;
FFT_K := 0;
FFT_E := 0;
else --Satır sonuna ulaşılmadı ise
--Bir sonraki satıra geç
--Küme ve dizi değişkenlerini sıfırla
FFT_S := FFT_S + 1;
FFT_K := 0;
FFT_E := 0;
end if;
else --Küme sonuna ulaşılmadı ise
--Bir sonraki kümeye geç
--Dizi değişkenini sıfırla
FFT_K := FFT_K + 1;
FFT_E := 0;
end if;
else --Eleman sonuna ulaşılmadı ise
--Bir sonraki elemana geç
FFT_E := FFT_E + 1;
end if;
end if;
end if;
end if; --rising_edge
end process;
end Behavioral;
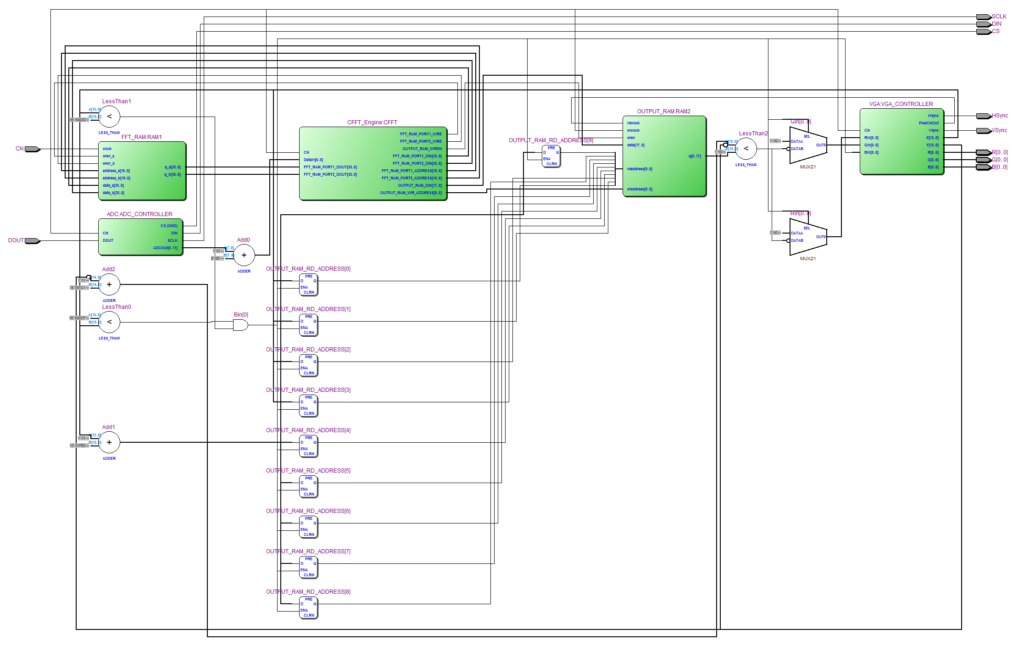
Quartus II programının oluşturduğu RTL şeması:
ADC ve VGA ile gerçekleştirilmiş 
noktalı CFFT uygulaması:
---------------------------------------------------------- -- CFFT_ADC.vhd -- Bertan Taşkın -- 2.6.2017 -- -- CFFT_Engine modülünü kullanak ADC'den alınan verilerin -- FFT'sini VGA ekranda görselleştiren uygulama -- -- ---------------------------------------------------------- --Kütüphaneler library IEEE; use IEEE.STD_LOGIC_1164.ALL; USE ieee.numeric_std.ALL; use ieee.math_real.all; entity CFFT_ADC is port(Clk : in std_logic; --Clock Girişi R, G, B : out std_logic_vector(0 downto 0); --VGA Arayüzünün Renk Sinyalleri HSync, VSync : out std_logic; --VGA Arayüzünün Senkronizasyon Sinyalleri CS, SCLK, DIN : out std_logic; --ADC Entegresinin kontrol Snyalleri DOUT : in std_logic); end CFFT_ADC; architecture Behavioral of CFFT_ADC is component CFFT_Engine generic(FFT_Power : integer := 3; --FFT Kuvveti Data_Width : integer := 8; --İşlenecek Verinin Boyutu Sampling_Cycle : integer := 250); --ADC İçin Sampling Cycle Süresi --FFT İçin Örnekleme Frekansı = Clk / Sampling_Cycle port(Clk : in std_logic; --Clock Girşi DataIn : in std_logic_vector(Data_Width - 1 downto 0); --ADC Veri Giriş Sinyali Reading : out std_logic; --ADC Okuması Yapılıp Yapılmadığını Belirten Sinyal DataIndex : out std_logic_vector(FFT_Power - 1 downto 0); --O Anki Okunan ADC Verisinin Sırası --FFT Hesaplmalarında Kullanılacak RAM'in Sinyalleri FFT_RAM_PORT1_DIN, FFT_RAM_PORT2_DIN : out std_logic_vector((Data_Width + FFT_Power) * 2 - 1 downto 0); --Veri Giriş Sinyalleri FFT_RAM_PORT1_DOUT, FFT_RAM_PORT2_DOUT : in std_logic_vector((Data_Width + FFT_Power) * 2 - 1 downto 0); --Veri Çıkış Sinyalleri FFT_RAM_PORT1_ADDRESS, FFT_RAM_PORT2_ADDRESS : out std_logic_vector(FFT_Power - 1 downto 0); --Adres Sinyalleri FFT_RAM_PORT1_WRE, FFT_RAM_PORT2_WRE : out std_logic; --Yazma Aktif Sinyalleri --Çıkış Verilerinin Tutulacağı RAM'in Sinyalleri OUTPUT_RAM_DIN : out std_logic_vector(Data_Width + FFT_Power - 1 downto 0); --Veri Giriş Sinyali OUTPUT_RAM_WR_ADDRESS : out std_logic_vector(FFT_Power - 2 downto 0); --Adres Sinyali OUTPUT_RAM_WREN : out std_logic); --Yazma Aktif Sinyali end component; --2048x36bit Dual-Port RAM --Single Clock, Çıkış asenkron component FFT_RAM PORT ( address_a : IN STD_LOGIC_VECTOR (10 DOWNTO 0); address_b : IN STD_LOGIC_VECTOR (10 DOWNTO 0); clock : IN STD_LOGIC := '1'; data_a : IN STD_LOGIC_VECTOR (35 DOWNTO 0); data_b : IN STD_LOGIC_VECTOR (35 DOWNTO 0); wren_a : IN STD_LOGIC := '0'; wren_b : IN STD_LOGIC := '0'; q_a : OUT STD_LOGIC_VECTOR (35 DOWNTO 0); q_b : OUT STD_LOGIC_VECTOR (35 DOWNTO 0) ); end component; --1024x18bit SemiDual-Port RAM --Dual Clock(Read-write), Çıkış asenkron component OUTPUT_RAM PORT ( data : IN STD_LOGIC_VECTOR (17 DOWNTO 0); rdaddress : IN STD_LOGIC_VECTOR (9 DOWNTO 0); rdclock : IN STD_LOGIC ; wraddress : IN STD_LOGIC_VECTOR (9 DOWNTO 0); wrclock : IN STD_LOGIC := '1'; wren : IN STD_LOGIC := '0'; q : OUT STD_LOGIC_VECTOR (17 DOWNTO 0) ); end component; --ADC kontrolcüsü component ADC port(Clk : in std_logic; --Clock Girişi CS, SCLK, DIN : out std_logic; --ADC Entegresinin CS, SCLK ve DIN Girişleri DOUT : in std_logic; --ADC Entegresinin DOUT Çıkışı ADCOut : out std_logic_vector(11 downto 0)); --ADC'den okunan 12 bitlik sinyal end component; --VGA kontrolcüsü component VGA generic(RGBLength : integer := 1); --R, G, B sinyallerinin genişliği --(Renk derinliği) port(Clk : in std_logic; --Clk girişi X, Y : out std_logic_vector(15 downto 0); --X,Y koordinatları --Bu sinyaller o an hangi pixelin DAC'ye --gönderileceğini belirtir. Rin, Gin, Bin : in std_logic_vector(RGBLength - 1 downto 0); --R, G, B bilgileri --Okunan X, Y sinyallerine göre istenen --RGB verisi bu sinyaller tarafında gönderilir. PixelClkOut : out std_logic; --Pixel Clock çıkışı --Monitöre giden sinyaller R, G, B : out std_logic_vector(RGBLength - 1 downto 0); --DAC'ye gönderilercek RGB sinyalleri HSync, VSync : out std_logic); --Yatay ve Dikey senkronizasyon sinyalleri end component; signal FFT_RAM_PORT1_DIN, FFT_RAM_PORT2_DIN : std_logic_vector(35 downto 0); signal FFT_RAM_PORT1_DOUT, FFT_RAM_PORT2_DOUT : std_logic_vector(35 downto 0); signal FFT_RAM_PORT1_ADDRESS, FFT_RAM_PORT2_ADDRESS : std_logic_vector(10 downto 0); signal FFT_RAM_PORT1_WRE, FFT_RAM_PORT2_WRE : std_logic; signal OUTPUT_RAM_DIN, OUTPUT_RAM_DOUT : std_logic_vector(17 downto 0); signal OUTPUT_RAM_WR_ADDRESS : std_logic_vector(9 downto 0); signal OUTPUT_RAM_RD_ADDRESS : std_logic_vector(9 downto 0); signal OUTPUT_RAM_WREN : std_logic; signal DataIn : std_logic_vector(6 downto 0); signal DataIndex : std_logic_vector(10 downto 0); signal Reading : std_logic; signal X, Y : std_logic_vector(15 downto 0); signal Rin, Gin, Bin : std_logic_vector(0 downto 0); signal Pixel_Clock : std_logic; signal ADC_Data : std_logic_vector(11 downto 0); begin --ADC verisinden 63 çıkartılarak [64,-63] aralığında veri elde edilir. --Bu şekilde AC bir sinyal elde edilir DataIn <= std_logic_vector(signed(unsigned(ADC_Data(11 downto 5))) - 63); --CFFT motorunun üretilmesi --2^11 = 2048 nokta --7 bit veri boyutu --50Mhz clock frekansı --250 sampling cycle: 50Mhz/250 = 200Khz --200Khz/2 = 100Khz spektrum --100khz/1024 = 97.7hz çözünürlük CFFT : CFFT_Engine generic map(11, 7, 250) port map(Clk, DataIn, Reading, DataIndex, FFT_RAM_PORT1_DIN, FFT_RAM_PORT2_DIN, FFT_RAM_PORT1_DOUT, FFT_RAM_PORT2_DOUT, FFT_RAM_PORT1_ADDRESS, FFT_RAM_PORT2_ADDRESS, FFT_RAM_PORT1_WRE, FFT_RAM_PORT2_WRE, OUTPUT_RAM_DIN, OUTPUT_RAM_WR_ADDRESS, OUTPUT_RAM_WREN); --FFT işleminde kullanılacak RAM'in üretilmesi RAM1 : FFT_RAM port map(FFT_RAM_PORT1_ADDRESS, FFT_RAM_PORT2_ADDRESS, Clk, FFT_RAM_PORT1_DIN, FFT_RAM_PORT2_DIN, FFT_RAM_PORT1_WRE, FFT_RAM_PORT2_WRE, FFT_RAM_PORT1_DOUT, FFT_RAM_PORT2_DOUT); --FFT işlemi sonucunda hesaplanan magnitude karelerin depolandığı RAM'in üretilmesi RAM2 : OUTPUT_RAM port map(OUTPUT_RAM_DIN, OUTPUT_RAM_RD_ADDRESS, Pixel_Clock, OUTPUT_RAM_WR_ADDRESS, Clk, OUTPUT_RAM_WREN, OUTPUT_RAM_DOUT); --VGA kontrolsünün üretilmesi VGA_CONTROLLER : VGA generic map(1) port map(Clk, X, Y, Rin, Gin, Bin, Pixel_Clock, R, G, B, HSync, VSync); --ADC kontrolcüsünün üretilmesi ADC_CONTROLLER : ADC port map(Clk, CS, SCLK, DIN, DOUT, ADC_Data); --VGA display'i kontrol eden process process(Pixel_Clock, X, Y, OUTPUT_RAM_DOUT) begin --Sağdan ve soldan 208 pixel boşluk bırakılır --(1440 - 1024) / 2 = 208 if unsigned(X) > 207 and unsigned(X) < 1232 then --OUTPUT_RAM'den o noktadaki FFT sonucu alınır OUTPUT_RAM_RD_ADDRESS <= std_logic_vector(unsigned(X) - 208)(9 downto 0); --Eğer FFT sonucu Y değerinin üzerinde ise pixele mavi bilgisi gönderilir if unsigned(OUTPUT_RAM_DOUT(16 downto 2)) > 899 - unsigned(Y) then Rin(0) <= '0'; Gin(0) <= '0'; Bin(0) <= '1'; else --Değil ise beyaz gönderilir Rin(0) <= '1'; Gin(0) <= '1'; Bin(0) <= '1'; end if; else --Çerçevenin dışında ise siyah gönderilir Rin(0) <= '0'; Gin(0) <= '0'; Bin(0) <= '0'; end if; end process; end Behavioral;
Quartus II programının oluşturduğu RTL şeması:
Kaynak kullanımı:
Toplam FFT cycle'ı: 
Cycle
Toplam FFT süresi: 
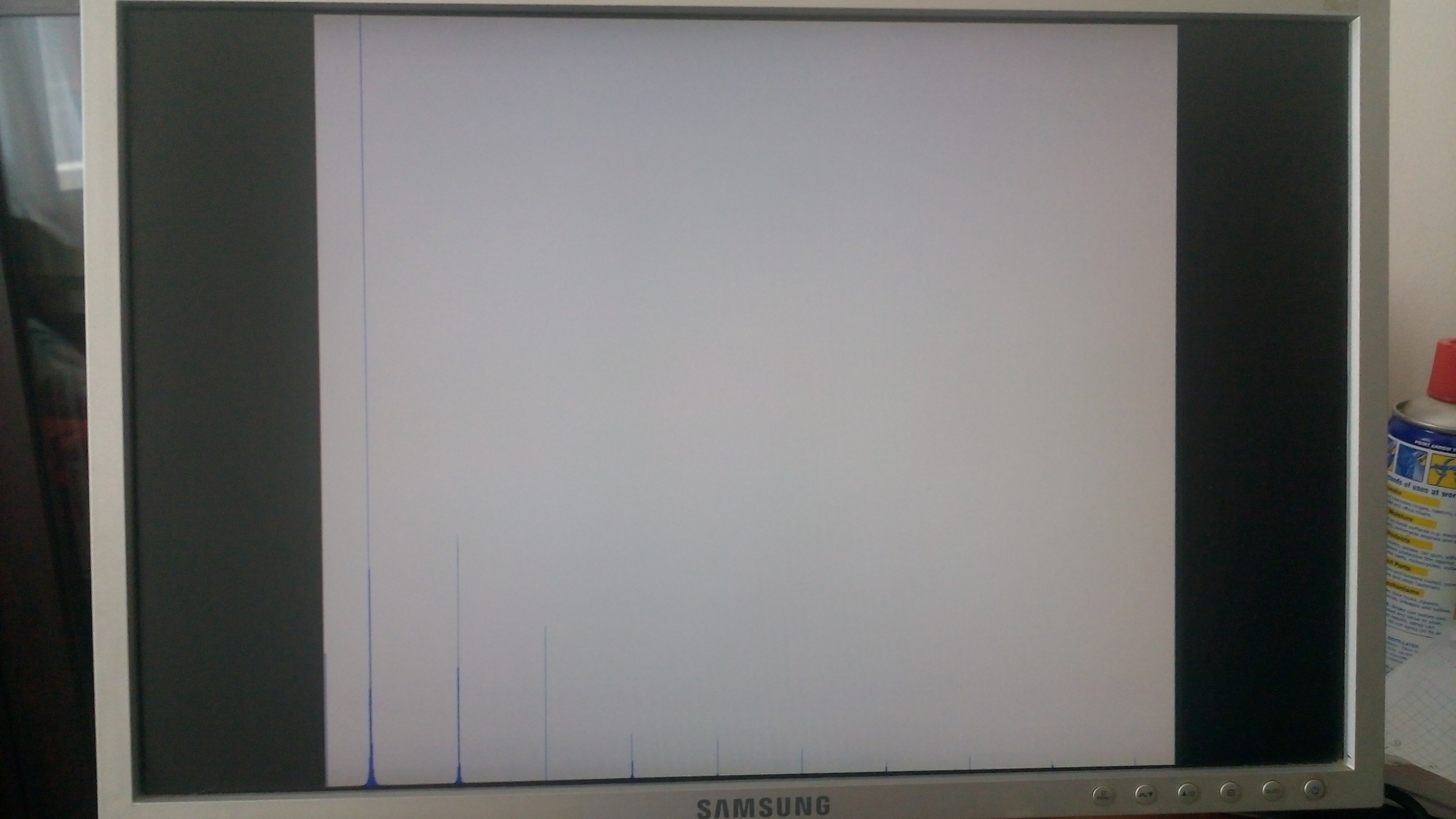
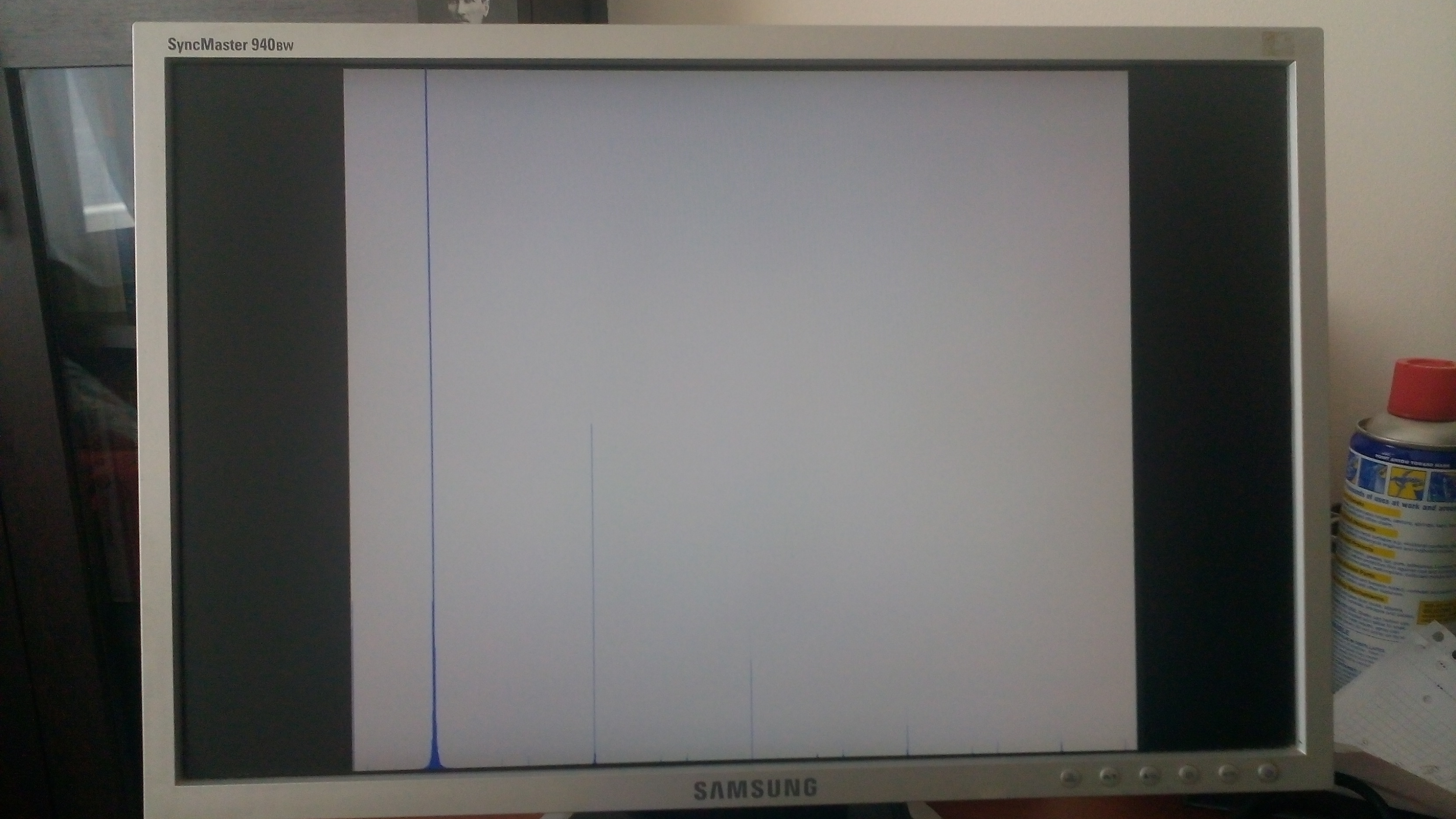
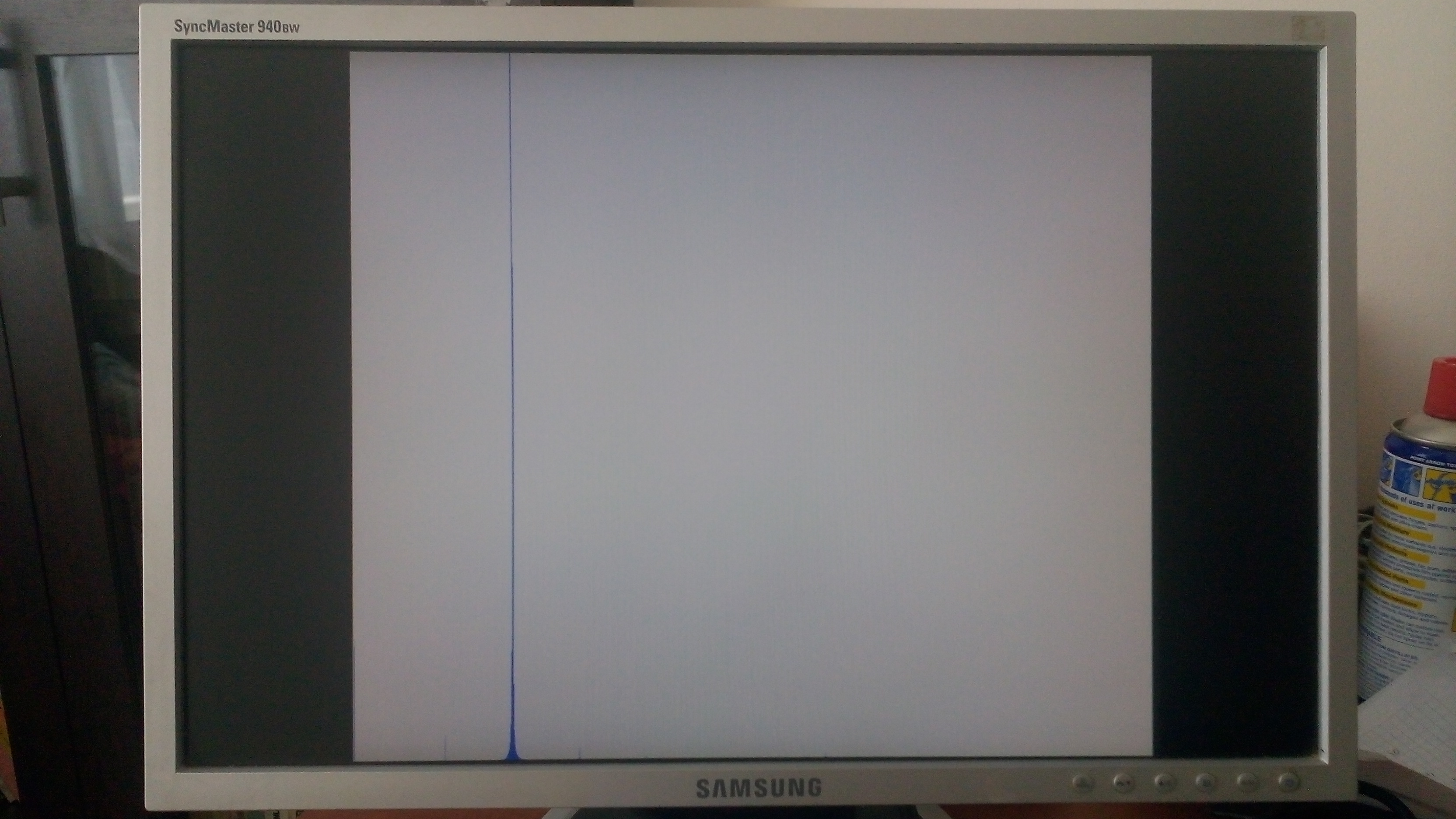
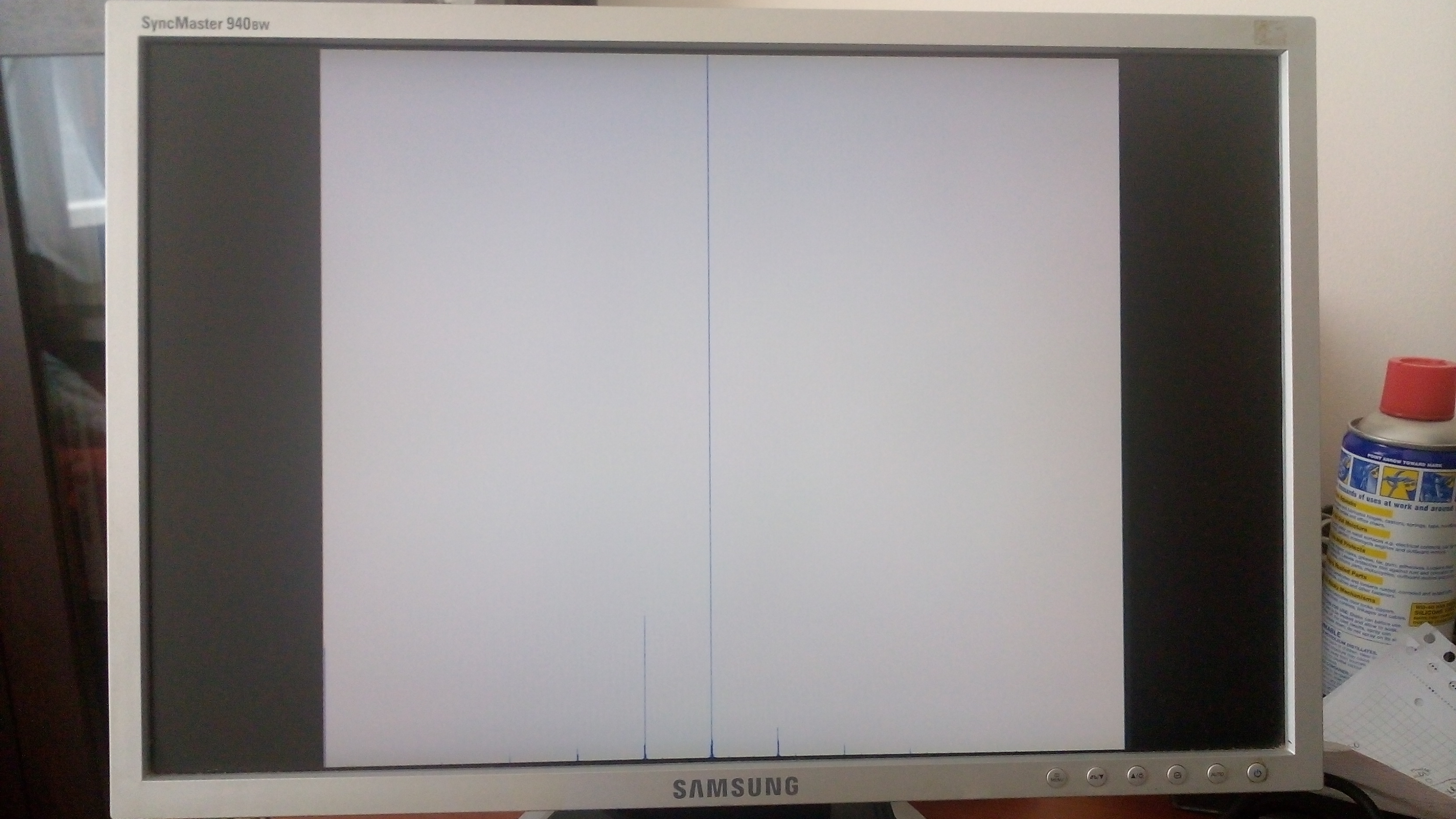
Kare dalga:
Kare Dalga:
Kare Dalga:
Sinüs Dalga:
Sinüs Dalga:
