FPGA Üzerinde CORDIC Algoritması ile Pipeline Tabanlı Magnitude ve Faz Açısı Hesaplama

CORDIC(COordinate Rotation Digital Computer) algoritması bir noktayı orjin etrafında döndürerek $\sin$ , $\cos$ , $\sinh$ , $\tan$ , $\tan^{-1}$ gibi fonksiyonları ve hatta $\alpha e^\theta$ , $\sqrt{x^2+y^2}$ , $\sqrt{x^2-y^2}$ gibi fonksiyonların da hesaplanmasını sağlayan bir algoritmadır.

Bu yazımda $\sqrt{x^2+y^2}$ (Magnitude) ve $\tan^{-1}\big(\frac{y}{x}\big)$ (Faz Açısı) hesaplaması üzerinde duracağım.

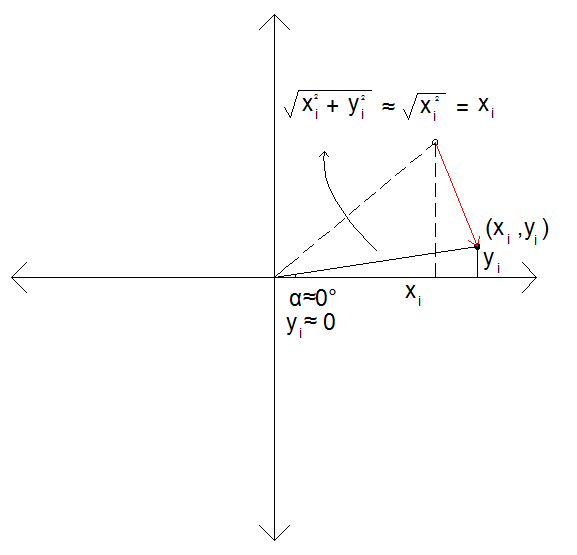
Kartezyen koordinat sisteminde bir $(x_0,y_0)$ noktası olsun. Bu noktanın magnitude değeri $\sqrt{x_0^2+y_0^2}$ 'dir.

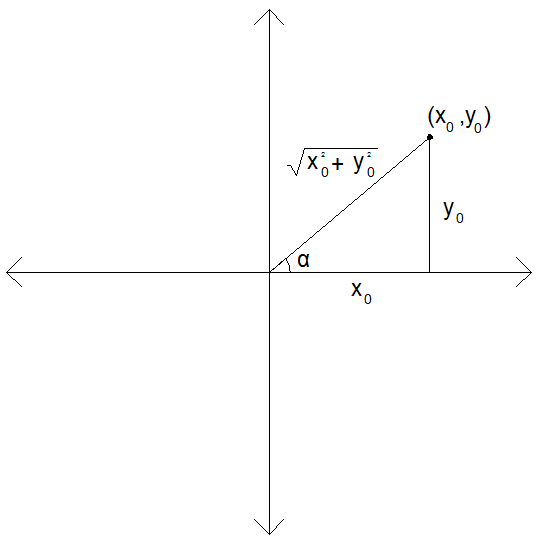
$\alpha$ açısını azalttığımızda $y_0$ değeri $y_0=x_0\tan(\alpha)$ olduğundan dolayı $0$ 'a yaklaşacaktır. $y_0$ değeri $0$ 'a yaklaşınca magnitude değeri de $\sqrt{x_i^2}=x_i$ 'ye yaklaşacaktır. $\alpha$ açısının değişmesi magnitude değerini etkilemediği için $x_i\approx\sqrt{x_0^2+y_0^2}$ diyebiliriz.

$(x_0,y_0)$ noktasını orjin etrafında( $z$ -ekseni etrafında) döndürmek için dönüşüm matrisi kullanılır.

Noktaları saat yönünün tersinde döndürmek istersek kullanacağımız dönüşüm matrisi:

$\begin{align*}\mathbf{R}_z(\theta)=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}\end{align*}$

$\begin{align*}\begin{bmatrix}x_{i+1}\\y_{i+1}\end{bmatrix}=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}\begin{bmatrix}x_{i}\\y_{i}\end{bmatrix}\end{align*}$

$\begin{align*}x_{i+1}=x_i\cos(\theta)-y_i\sin(\theta)\\y_{i+1}=y_i\cos(\theta)+x_i\sin(\theta)\end{align*}$

$\begin{align*}x_{i+1}=\cos(\theta)[x_i-y_i\tan(\theta)]\\y_{i+1}=\cos(\theta)[y_i+x_i\tan(\theta)]\end{align*}$

Elimizde $\theta=\tan^{-1}(2^{-i}),\,i:0\to n$ değerlerinin tutulduğu bir tablomuz olsun.

$\begin{align*}\cos(\theta)=\frac{1}{\sqrt{2^{-2i}+1}}=G_i\end{align*}$

$\begin{align*}\tan(\theta)=2^{-i}\end{align*}$

$\begin{align*}x_{i+1}=G_i[x_i-y_i\,2^{-i}]\\y_{i+1}=G_i[y_i+x_i\,2^{-i}]\end{align*}$

$2^{-i}$ işlemi bilgisayarlarda basit bit kaydırma ile yapılabilir.

Koordinatları orjin etrafında saat yönünün tersinde döndürürken $\alpha$ açısı yani faz açısının değerini de her bir dönüşümden sonrada $\theta=\tan^{-1}(2^{-i})$ çıkarmamız gerekir.

$\begin{align*}z_{i+1}=z_i-\theta=z_i-tan^{-1}(2^{-i})\end{align*}$

Eğer noktaları orjin etrafında saat yönünde döndürmek istersek:

$\begin{align*}x_{i+1}=G_i[x_i+y_i\,2^{-i}]\\y_{i+1}=G_i[y_i-x_i\,2^{-i}]\\z_{i+1}=z_i+tan^{-1}(2^{-i})\end{align*}$

Noktaları hangi yöne döndüreceğimizi $y_i$ 'nin değeri ile anlayabiliriz. Eğer $y_i<0$ ise $(x_i,y_i)$ noktası koordinat sisteminin sağ alt çeyreğindedir ve saat yönünün tersinde dönüşüm yapmamız gerekir. $y\geq0$ ise de saat yönünde dönüşüm yapmamız gerekir.

Genel olarak algoritmayı şu şekilde yazabiliriz:

$\begin{align*}x_{i+1}=G_i[x_i-d_i\,y_i\,2^{-i}]\\y_{i+1}=G_i[y_i+d_i\,x_i\,2^{-i}]\\z_{i+1}=z_i-d_i\,tan^{-1}(2^{-i})\end{align*}$

$\begin{align*}d_i=\begin{cases}+1,\,\,\,\,\,\,\,y_i<0\\-1,\,\,\,\,\,\,\,\text{diger}\end{cases}\end{align*}$

$G_i$ değeri her iterasyonda gelen kazançtır. Bütün işlemler bittikten sonra $x_n$ değeri bütün iterasyonların ters kazancı olan $K_n=\frac{1}{G}$ ile çarpılarak kazanç $1$ 'e düşürülür.

FPGA üzerinde uygulanması

Birden çok nokta ile çalışırken, her bir nokta için teker teker algoritmayı uygulamak fazla clock cycle'ı harcamamıza neden olur. Pipeline tasarım ile bu soruna çözüm üretilebilir.

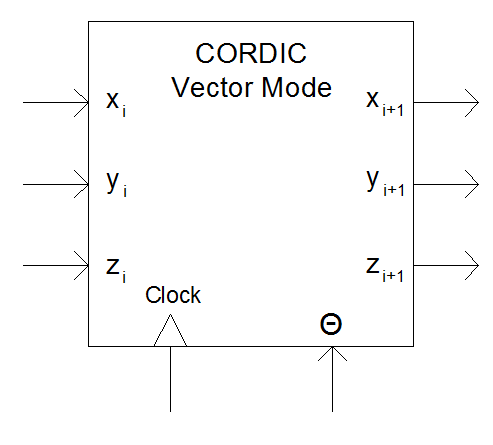
Pipeline yapı CORDIC çekirdeklerinin birbirine seri bağlanması ile yapılır. Her bir çekirdek aşağıdaki gibidir:

Tasarımın VHDL kodu:

----------------------------------------------------------
--                   CORDIC_VectorMode.vhd
--                       Bertan Taşkın
--                         2.6.2017
--
-- Pipeline tabanlı çalışmaya tasarlanmış, Vectör modunda
-- çalışan CORDIC çekirdeği modülü. İşlenecek veri boyutu
-- generic kısmındaki Data_Width ile belirlenir. Pipeline'ın
-- hangi adımında olduğu ise PipelineStage ile belirlenir.
-- Clock sinyalinin yükselen kenarı ile işlenmiş X,Y,Zin
-- verileri pipeline'daki bir sonraki çekirdeğe aktarılır.
-- 
-- Faz açısı 1 işaret biti ve Data_Width-1 kadar fraction
-- bitinden oluşur. Radyan cinsinden çıkış verir.
--
-- Data_Width değerinin alabileceği en yüksek değer integer
-- genişliği olan 32'dir.
--
--
----------------------------------------------------------


--Kütüphaneler
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
USE ieee.numeric_std.ALL; 
use ieee.math_real.all;

entity CORDIC_VectorMode is
	generic(Data_Width : integer := 16;                                    --İşlenecek Veri Genişliği
		PipelineStage : integer := 8);                                     --Çekirdeğin Bulunduğu Pipeline Seviyesi
		
	port(Clk : in std_logic;		                                       --Clock Girişi
		Xin, Yin, Zin : in std_logic_vector(Data_Width - 1 downto 0);      --Önceki CORDIC Çekirdeğinden Gelen X, Y, Z Girişleri
		Xout, Yout, Zout : out std_logic_vector(Data_Width - 1 downto 0)); --Sonraki CORDIC Çekirdeğine Gidecek X, Y, Z Çıkışları
end CORDIC_VectorMode;

architecture Behavioral of CORDIC_VectorMode is
	
	signal XS, YS, ZS : signed(Data_Width - 1 downto 0);
	
	--Phase hesabında kullanılacak arctanjant değeri
	--[-0.5, 0.5] aralığına normalize ediliyor
	constant AtanReal : real := ARCTAN(real(2) ** real(-PipelineStage)) * real(2**(Data_Width - 1)) / MATH_PI;
	signal Atan : signed(Data_Width - 1 downto 0);
	
begin

	--İşlemlerin daha kolay yapılabilmesi için giriş
	--sinyalleri signed tipine dönüştürülüyor
	XS <= signed(Xin);
	YS <= signed(Yin);
	ZS <= signed(Zin);
	
	--Arctanjant değeri de signed tipine dönüştürülüyor
	Atan <= to_signed(integer(AtanReal), Data_Width);
	
	--CORDIC işleminin gerçekleştiği process
	process(Clk)
	begin
		--Clock sinyalinin yükselen kenarı ile Pipeline ilerler
		if rising_edge(Clk) then
			
			--Eğer Ys değeri 0'dan küçük ise koordinatlar saat yönünün
			--tersinde döndürülüyor
			if Ys < 0 then
				--Signed tipinden tekrar std_logic_vector tipine dönüştürülüyor
				Xout <= std_logic_vector(XS - shift_right(YS, PipelineStage));
				Yout <= std_logic_vector(YS + shift_right(XS, PipelineStage));
				Zout <= std_logic_vector(ZS - Atan);
				
			--Değil ise saat yönünde döndürülüyor
			else
				Xout <= std_logic_vector(XS + shift_right(YS, PipelineStage));
				Yout <= std_logic_vector(YS - shift_right(XS, PipelineStage));
				Zout <= std_logic_vector(ZS + Atan);
			end if;
		end if;
	end process;

end Behavioral;

Quartus II tarafından oluşturulan RTL şeması:

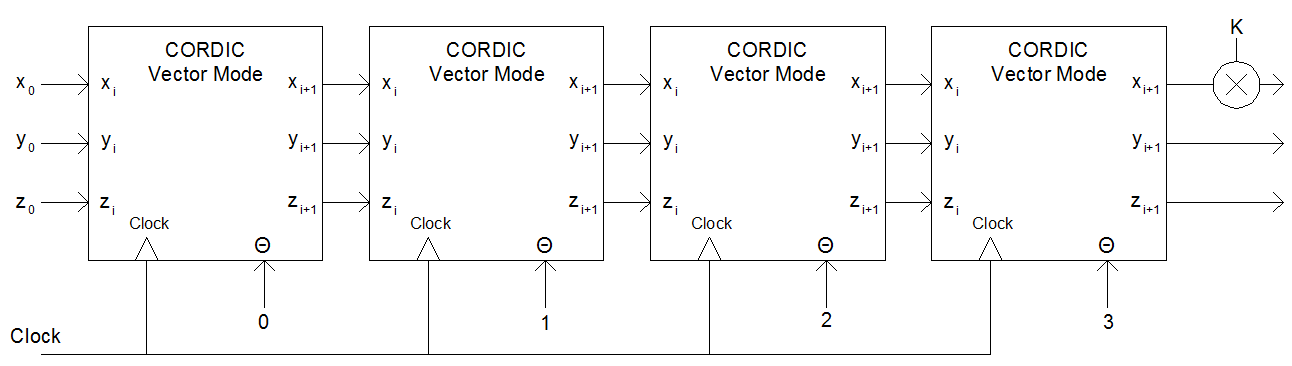
Çekirdeklerin seri bağlanmış hali:

Tasarımın VHDL kodu:

----------------------------------------------------------
--                   CORDIC_MagPha.vhd
--                     Bertan Taşkın
--                       2.6.2017
--
-- CORDIC algoritmasını kullanarak (X,Y) noktası için
-- magnitude'u ve faz açısını hesaplayan modül. Pipeline
-- yapıya sahiptir. İşlenecek veri boyutu generic kısmındaki
-- Data_Width ile belirlenir. Pipeline uzunluğu ise PipelineLength
-- ile belirlenir.
--
-- Modül pipeline tabanlı olduğundan dolayı, yeni veriler
-- PipelineStage kadar gecikmeli hesaplanır. Sıralı giren veri
-- sayısı ne kadar fazla olursa verimlilik de o kadar yüksek olur.
--
-- N veri için toplam işlem süresi = PipelineStage + N - 1 Cycle 
--
-- Giriş verilerinde kesinlikle fraction part bırakılmalıdır.
-- Toplam pipeline adım sayısı, giriş verilerinin fraction bit
-- sayısından 1 fazlasından fazla olması yüksek pipeline
-- adımlarının hassasiyetini düşürür.
--
-- Magnitude = MagnitudeOut / 2^Fraction_Bit_Sayısı
--
-- Faz açısı 1 işaret bitinden ve Data_Width-1 fraction bitinden
-- oluşur. [-0.5, 0.5] aralığında radyan cinsindendir.
--
-- Faz açısı = PhaseOut / 2^(Data_Width-1) Radyan
--           = PhaseOut / 2^(Data_Width-1) * 180 Derece
--
----------------------------------------------------------


--Kütüphaneler
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
USE ieee.numeric_std.ALL; 
use ieee.math_real.all;

entity CORDIC_MagPha is
	generic(Data_Width : integer := 16;                               --İşlenecek Veri Genişliği
		PipelineLength : integer := 9);                               --Pipeline Uzunluğu(Derinliği)
		
	port(Clk : in std_logic;                                          --Clock Girişi
		X, Y : in std_logic_vector(Data_Width - 1 downto 0);          --X, Y Girişleri
		MagnitudeOut : out std_logic_vector(Data_Width - 1 downto 0); --Magnitude Çıkışı
		PhaseOut : out std_logic_vector(Data_Width - 1 downto 0));    --Faz açısı Çıkışı
end CORDIC_MagPha;

architecture Behavioral of CORDIC_MagPha is
	
	--CORDIC algoritmasının kazancını 1'e düşürecek Kn değerini
	--hesaplayan fonksiyon
	--Kn = pi i:0->n 1/kök(1+2^(-2i))
	function Kn(n : integer) return signed is
	variable X : signed(Data_Width - 1 downto 0) := (others=>'0');
	variable K : real := 1.0;
	begin

		--Her bir CORDIC çekirdeğinin kazancının tersi çarpılarak
	    --Kn değeri hesaplanır
		a : for i in 0 to n loop
			K := K / SQRT((real(1) + real(2) ** real(-2 * i)));
		end loop;
		
		--K sayısı, Data_Width kadar fraction bit sayısına sahip
		--fixed-point sayıya dönüştürülüyor
		K := K * real(2**(Data_Width - 1));
		
		X := to_signed(integer(K), Data_Width);
		
		return X;
	end Kn;
	
--Vectör modundaki CORDIC çekirdeği
component CORDIC_VectorMode
	generic(Data_Width : integer := 16;                                    --İşlenecek Veri Genişliği
		PipelineStage : integer := 8);                                     --Çekirdeğin Bulunduğu Pipeline Seviyesi
		
	port(Clk : in std_logic;		                                       --Clcok Girişi
		Xin, Yin, Zin : in std_logic_vector(Data_Width - 1 downto 0);      --Önceki CORDIC Çekirdeğinden Gelen X, Y, Z Girişleri
		Xout, Yout, Zout : out std_logic_vector(Data_Width - 1 downto 0)); --Sonraki CORDIC Çekirdeğine Gidecek X, Y, Z Çıkışları
end component;
	
	type VectorArray is array(PipelineLength downto 0) of std_logic_vector(Data_Width - 1 downto 0);
	signal XBus, YBus, ZBus : VectorArray;
	
begin

	--CORDIC algoritmasının doğru çalışması için girilen koordinatların
	--koordinat ekseninin sağ düzleminde(-pi/2 < açı < pi/2) olması gerekir.
	--Eğer X koordinatı negatif ise (X,Y) noktası koordinat ekseninin sol
	--tarafındadır. Bunu düzeltmek için sonucu değiştirmeyen (-X,-Y) noktası
	--ile işleme devam edilir.
	with X(Data_Width - 1) select
		XBus(0) <= not X when '1',
					  X when others;
					  
	with X(Data_Width - 1) select
		YBus(0) <= not Y when '1',
					  Y when others;

	--İşlem öncesi (X,Y) noktası döndürülmeyeceğinden Z açısı 0 ile başlar
	ZBus(0) <= (others=>'0');

	--Son CORDIC çekirdeğinden çıkan Magnitude değeri, algoritmadan
	--kaynaklanan kazancı 1'e çekmek için Kn ile çarpılır
	MagnitudeOut <= std_logic_vector(shift_right(signed(XBus(PipelineLength)) * Kn(PipelineLength - 1), Data_Width - 1))(Data_Width - 1 downto 0);
	
	--Faz açısında herhangi bir ek işleme gerek yoktur
	PhaseOut <= ZBus(PipelineLength);

	--CORDIC çekirdeklerinin üretilmesi
	--Bütün CORDIC çekirdekleri birbirine seri bağlanır(Pipeline yapısı)
	U1: for i in 0 to PipelineLength - 1 generate
		CORDIC_Core: CORDIC_VectorMode
			generic map(Data_Width, i)
			port map(Clk,
				XBus(i), YBus(i), ZBus(i),
				XBus(i + 1), YBus(i + 1), ZBus(i + 1));
	end generate;


end Behavioral;

RTL şeması:

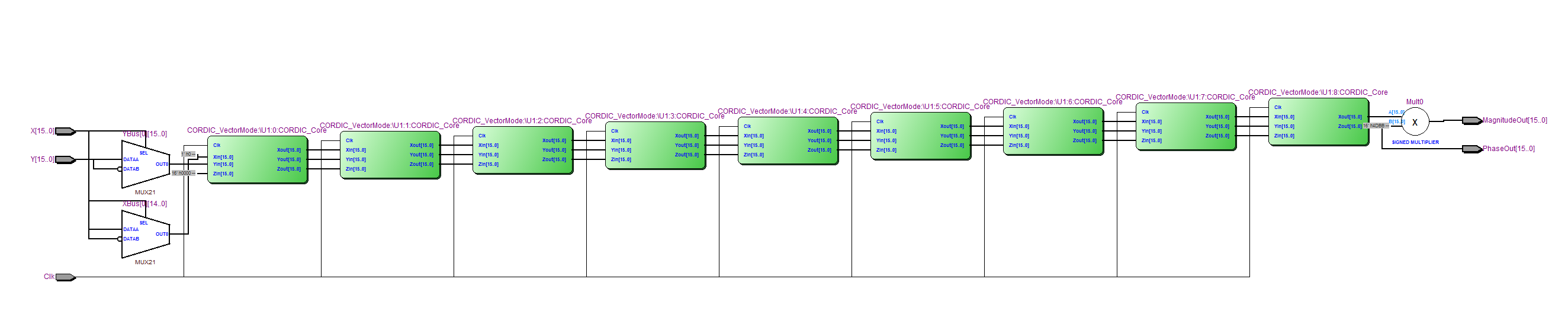
Kaynak kullanımı:

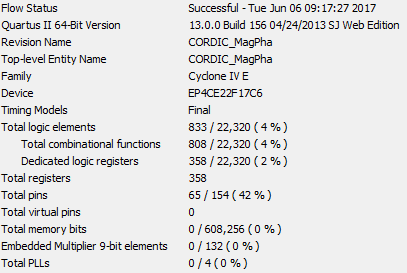8 biti fraction olmak üzere 16-bit veri genişliği ve 9 pipeline derinliğine sahip uygulamanın ModelSim ile gerçekleştirilen testi:

1.Veri:

Giriş: $x_0=(\text{0300})_{16}\times2^{-8}=3\,,\,y_0=(\text{0400})_{16}\times2^{-8}=4$

Çıkış: $Mag=(\text{0500})_{16}\times2^{-8}=5\,,\,Pha=(\text{25E8})_{16}\times2^{-15}\times180^\circ=53.305664^\circ$

Gerçek değer: $Mag=5\,,\,Pha=53.130102^\circ$

2.Veri:

Giriş: $x_0=(\text{0400})_{16}\times2^{-8}=4\,,\,y_0=(\text{FBFF})_{16}\times2^{-8}=-4$

Çıkış: $Mag=(\text{05A8})_{16}\times2^{-8}=5.65625\,,\,Pha=(\text{E022})_{16}\times2^{-15}\times180^\circ=-44.813232^\circ$

Gerçek değer: $Mag=5.656854\,,\,Pha=-45^\circ$

3.Veri:

Giriş: $x_0=(\text{FAFF})_{16}\times2^{-8}=-5\,,\,y_0=(\text{0C00})_{16}\times2^{-8}=12$

Çıkış: $Mag=(\text{0D02})_{16}\times2^{-8}=13.007812\,,\,Pha=(\text{CFF6})_{16}\times2^{-15}\times180^\circ=-67.554931^\circ$

Gerçek değer: $Mag=13\,,\,Pha=-67.380135^\circ$

4.Veri:

Giriş: $x_0=(\text{D9FF})_{16}\times2^{-8}=-38\,,\,y_0=(\text{F8FF})_{16}\times2^{-8}=-7$

Çıkış: $Mag=(\text{26A4})_{16}\times2^{-8}=38.640625\,,\,Pha=(\text{0768})_{16}\times2^{-15}\times180^\circ=10.415039^\circ$

Gerçek değer: $Mag=38.639358\,,\,Pha=10.437475^\circ$

Bir cevap yazın Cevabı iptal et