Cooley-Tukey FFT Algoritması J.W. Cooley ve John Tukey tarafından geliştirilen hızlandırılmış fourier dönüşümü algoritmalarından biridir.
 nokta için DFT şu şekilde tanımlanır:
nokta için DFT şu şekilde tanımlanır:

Her bir  değeri için
değeri için  tane complex çarpma işlemi gerekir. Toplamda
tane complex çarpma işlemi gerekir. Toplamda  tane
tane  değeri hesaplanacağından, DTF'nin bu hali için işlem süresi
değeri hesaplanacağından, DTF'nin bu hali için işlem süresi  olur.
olur.
DFT'yi  ve
ve  olacak şekilde
olacak şekilde  parçaya ayıralım.
parçaya ayıralım.




Burada 
 terimlerinin DFT'si,
terimlerinin DFT'si,  ise
ise  terimlerinin DFT'sidir.
terimlerinin DFT'sidir.
DFT'nin özelliği gereği  eşitliği vardır:
eşitliği vardır:



Burada  ifadesi Twiddle Factor olarak adlandırılır ve
ifadesi Twiddle Factor olarak adlandırılır ve  şeklinde gösterilir.
şeklinde gösterilir.


 DFT'sini
DFT'sini  ve
ve  'li terimlerini ayrı ayrı hesaplayalım.
'li terimlerini ayrı ayrı hesaplayalım.




Aynı şekilde  içinde hesap yaparsak:
içinde hesap yaparsak:




Bu işlemleri  kere tekrarlarsak:
kere tekrarlarsak:

Toplam sembolünün içerisindeki twiddle factor'ler  'e eşit olduğundan dolayı
'e eşit olduğundan dolayı  tane complex çarpma işlemi yok edilmiş olur. Cooley Tukey algorimasının hızlanmasını sağlayan bu terimlerin yok edilmesidir.
tane complex çarpma işlemi yok edilmiş olur. Cooley Tukey algorimasının hızlanmasını sağlayan bu terimlerin yok edilmesidir.


 için Cooley-Tukey Algoritmasının Şematik Gösterimi:
için Cooley-Tukey Algoritmasının Şematik Gösterimi:
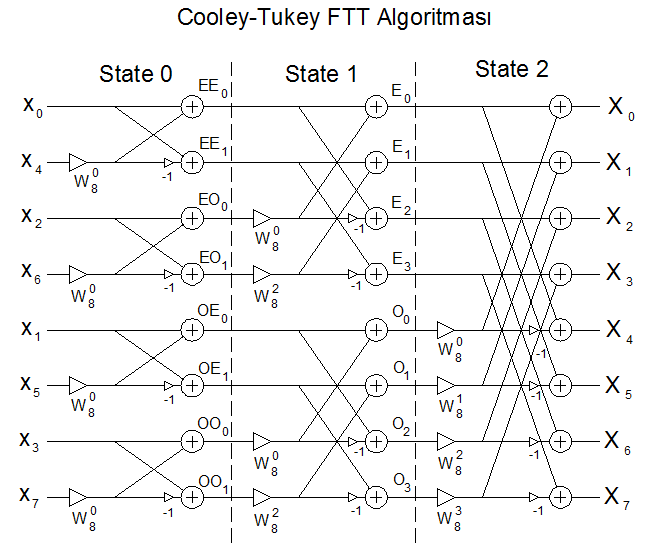 Yukarıdaki şemadan da görüleceği gibi her bir state'de
Yukarıdaki şemadan da görüleceği gibi her bir state'de  adet complex çarpma işlemi yapılır. Toplam state sayısı ise
adet complex çarpma işlemi yapılır. Toplam state sayısı ise  'dir. Bu durumda Cooley-Tukey algoritması ile DFT'nin çalışma süresi
'dir. Bu durumda Cooley-Tukey algoritması ile DFT'nin çalışma süresi  'e düşürülmüş olur.
'e düşürülmüş olur.
Normal DFT ile Cooley-Tukey DFT'nin Nokta Sayısı-İşlem Yükü Karşılaştırması: