Floating Point Aritmetiği ve FPGA Üzerinde Çarpma İşleminin Gerçekleştirilmesi

Floating point sayı formatı reel sayıları saklamak için kullanılan formatlardan biridir. Fixed point'den farkı ondalık işaretinin sabit olmamasıdır. Fixed point sayılar binary formda $\text{xx.xxxxx}$ şeklinde saklanıp ondalık tabanda,

$\begin{align*}\sum_{n=0}^p\end{align*}m_n\times2^{k-n}\,\,\,,\,\,\,p,k\in\mathbb{Z}^{+}$

şekline ifade edilir.

Floating pointde ise sayılar eksponansiyel olarak $(-1)^\mathrm{s}\times\mathrm{m}\times2^\mathrm{e}$ şeklinde ifade edilir. Burada $\mathrm{s}$ significand (işaret biti), $\mathrm{e}$ exponent ve $\mathrm{m}$ mantissa olarak adlandırılır. Binary formda ise,

$\begin{align*}\underbrace{s}_\text{significand}\underbrace{e_{k-1}\,e_{k-2}\,\dots\,e_{0}}_\text{exponent}\,\underbrace{m_{p-1}\,m_{p-2}\,\dots\,m_{0}}_\text{matissa}\end{align*}$

şeklinde saklanır. Exponent ve mantissa bitlerinin sayısı değiştirilerek hassasiyet ve sınır ayarlanablir.

IEEE754 standartındaki floating point formatları:

Half Precision: 5 Exponent biti, 10 Mantissa biti. Onluk tabanda $\approx3.3$ basamak.
Single Precision: 8 Exponent biti, 23 Mantissa biti. Onluk tabanda $\approx7.2$ basamak.
Double Precision: 11 Exponent biti, 64 Mantissa biti. Onluk tabanda $\approx15.9$ basamak.
Quad Precision: 15 Exponent biti, 112 Mantissa biti. Onluk tabanda $\approx34$ basamak.

Floating point sayılar onluk tabanda,

$\begin{align*}\Bigg(1+\sum_{n=1}^{k-1}\,\mathrm{m}_n\times2^{-n}\Bigg)\,\times\,2^\mathrm{(e-bias)}\end{align*}$

ile ifade edilir. Burada bias değeri, $k$ exponent biti için $2^{k-1}$ 'dir.

Exponent ile ilgili 3 tane özel durum vardır:

1.Denormalize Sayı

Exponent'in $0$ olması durumudur. Bu durumda sayı onluk tabanda,

$\begin{align*}\Bigg(\sum_{n=1}^{k-1}\,\mathrm{m}_n\times2^{-n}\Bigg)\,\times\,2^\mathrm{(e-bias)}\end{align*}$

şeklinde ifade edilir.

2.Sonsuz

Exponent'in bütün bitlerinin $'1'$ ve mantissa'nın $0$ olması durumudur.

3.NaN (Not a Number)

Exponent'in bütün bitlerinin $'1'$ ve mantissa'nın $0$ 'dan farklı olması durumudur.

Floating Point Sayılarda Çarpma İşleminin Gerçekleştirilmesi

$\begin{align*}f_3=f_1\times f_2\end{align*}$

$\begin{align*}f_3=\Big[(-1)^{\mathrm{s}_1}\times\mathrm{m}_1\times2^{\mathrm{e}_1}\Big]\times\Big[(-1)^{\mathrm{s}_2}\times\mathrm{m}_2\times2^{\mathrm{e}_2}\Big]\end{align*}$

$\begin{align*}f_3=(-1)^{\mathrm{s}_1\oplus\mathrm{s}_2}\times(\mathrm{m}_1\times\mathrm{m}_2)\times2^{\mathrm{e}_1+\mathrm{e}_2}\end{align*}$

Görüldüğü gibi significand bitlerinin xor işlemine sokulması, mantissaların çarpılması ve exponentlerin toplanması ile çarpma işlemi gerçekleştirilir. Mantissalar çarpılırken taşma olursa exponent değeri $1$ arttırılır, bu işlem ön normalizasyon olarak da geçer. Ön normalizasyon işleminden sonra yuvarlama işlemleri gelir. $4$ farklı yuvarlama tipi vardır. Bunlar:

Sıfıra yuvarlama
En yakın çift sayıya yuvarlama
Pozitif sonsuza yuvarlama
Negatif sonsuza yuvarlama'dır.

IEEE754 standartında varsayılan mod en yakın çift sayıya yuvarlamadır. Yuvarlama yapılırken mantissaların çarpımından hesaplanan round, sticky (ve bazen de guard) bitleri kullanılır.

Yuvarlama sonunda mantissada taşma olursa exponent $1$ arttırılır. Bu işleme de son normalizasyon denir.

Normalisayon işlemleri sırasında exponentde de taşma olur ise sayı sonsuz durumuna gelir.

FPGA Üzerinde Çarpma İşleminin Gerçekleştirilmesi

Blok Diagramı:

VHDL Kodu:

------------------- FloatingPoint_Multiplication.vhd ---------------
--                           Bertan Taşkın
--                             16.7.2017
--
-- Floating Point sayılarda çarpma işlemini gerçekleştiren modül.
-- Exponent ve Mantissa bitlerinin sayısı generic kısmından değiştirilerek
-- özel formatlar yaratılabilir. İşlemler pipeline tabanlı yapılır.
--
-- IEEE754 Standartları:
--                                             Onluk Tabandaki
--                     Exponent    Mantissa     Basamak Sayısı
-- Half Precision        5           10              ~3.3
-- Single Precision      8           23              ~7.2
-- Double Precision     11           52             ~15.9
-- Quad Precision       15          112             ~34
--
-- Yuvarlama Tipleri:
-- 
-- Sıfıra yuvarlama               : "00"
-- En yakın çift sayıya yuvarlama : "01"
-- Pozitif sonsuza yuvarlama      : "10"
-- Negatif sonsuza yuvarlama      : "11"
--
-- Pipeline gecikmesi = 5 Cycle
--


--Kütüphaneler
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
USE ieee.numeric_std.ALL; 
use ieee.math_real.all;

entity FloatingPoint_Multiplication is
	generic(Exponent : natural := 8;                        --Exponent Bit Sayısı
		Mantissa : natural := 23);                          --Mantissa Bit Sayısı
		
	port(Clk, Enable : in std_logic;                        --Clock ve Enable Girişleri
		RoundingMode : in std_logic_vector(1 downto 0);     --Yuvarlama Tipi
		F1, F2 : in unsigned(Exponent + Mantissa downto 0); --Giriş Değerleri
		F3 : out unsigned(Exponent + Mantissa downto 0);    --Çıkış Değeri
		Exception_Inf, Exception_NaN : out std_logic);      --Özel Değer Bayrakları
end FloatingPoint_Multiplication;

architecture Behavioral of FloatingPoint_Multiplication is

	--Exponent'in Bias değeri 
	constant Bias : unsigned := to_unsigned(2**(Exponent - 1) - 1, Exponent);
	
	--Özel Değerler
	constant SpecialExpoent : unsigned(Exponent - 1 downto 0) := (Exponent - 1 downto 0 => '1');
	constant ZerosExponent : unsigned(Exponent - 1 downto 0) := (Exponent - 1 downto 0 => '0');
	constant ZerosMantissa : unsigned(Mantissa - 1 downto 0) := (Mantissa - 1 downto 0 => '0');
	constant OnesMantissa : unsigned(Mantissa - 1 downto 0) := (Mantissa - 1 downto 0 => '1');							
	
	--Denormalize exponent
	constant DenormalizeExponent : unsigned(Exponent - 1 downto 0) := (others=>'0');
	
	--Yuvarlama tipleri
	constant RoundtoZero : std_logic_vector(1 downto 0) := "00";
	constant RoundtoNearestEven : std_logic_vector(1 downto 0) := "01";
	constant RoundtoPlusInfinity : std_logic_vector(1 downto 0) := "10";
	constant RoundtoMinusInfinity : std_logic_vector(1 downto 0) := "11";
	
	--Özel durumlar
	constant NoException : std_logic_vector(1 downto 0) := "00";
	constant Infinity : std_logic_vector(1 downto 0) := "01";
	constant NotaNumber : std_logic_vector(1 downto 0) := "10";
	
	--Sayının NaN olup olmadığını kontrol eden fonksiyon
	function IsNaN(FP : unsigned) return std_logic is
	begin
		if FP(Exponent + Mantissa - 1 downto Mantissa) = SpecialExpoent and
			FP(Mantissa - 1 downto 0) /= ZerosMantissa then
			return '1';
		else
			return '0';
		end if;
	end function;
	
	--Sayının sonsuz olup olmadığını kontrol eden fonksiyon
	function IsInf(FP : unsigned) return std_logic is
	begin
		if FP(Exponent + Mantissa - 1 downto Mantissa) = SpecialExpoent and
			FP(Mantissa - 1 downto 0) = ZerosMantissa then
			return '1';
		else
			return '0';
		end if;
	end function;
	
	--Sayının sıfır olup olmadığını kontrol eden fonksiyon
	function IsZero(FP : unsigned) return std_logic is
	begin
		if FP(Exponent + Mantissa - 1 downto Mantissa) = ZerosExponent and
			FP(Mantissa - 1 downto 0) = ZerosMantissa then
			return '1';
		else
			return '0';
		end if;
	end function;
	
	--Takma adlar
	alias F1_Sign is F1(Exponent + Mantissa);
	alias F1_Exponent is F1(Exponent + Mantissa - 1 downto Mantissa);
	alias F1_Mantissa is F1(Mantissa - 1 downto 0);
	
	alias F2_Sign is F2(Exponent + Mantissa);
	alias F2_Exponent is F2(Exponent + Mantissa - 1 downto Mantissa);
	alias F2_Mantissa is F2(Mantissa - 1 downto 0);
	
	alias F3_Sign is F3(Exponent + Mantissa);
	alias F3_Exponent is F3(Exponent + Mantissa - 1 downto Mantissa);
	alias F3_Mantissa is F3(Mantissa - 1 downto 0);
	
	
	signal s1, s2, s3 : std_logic := '0';
	signal e1, e2, e3 : unsigned(Exponent - 1 downto 0) := (others=>'0');
	signal m1, m2, m3 : unsigned(Mantissa downto 0) := (others=>'0');
	
	signal s1s2, s1s2_2 : std_logic := '0';
	signal e1e2, e1e2_2 : unsigned(Exponent - 1 downto 0) := (others=>'0');
	signal m1m2, m1m2_2 : unsigned(Mantissa downto 0) := (others=>'0');
	
	signal Exception, Exception_2, Exception_3, Exception_4 : std_logic_vector(1 downto 0) := "00";
	
	signal RoundBit, StickyBit : std_logic := '0';
	
begin

	process(Clk, Enable)
	variable m1m2Signal : unsigned(Mantissa * 2 + 1 downto 0) := (others=>'0');
	variable Rounded_m1m2 : unsigned(Mantissa downto 0) := (others=>'0');
	begin
		
		if rising_edge(Clk) and Enable = '1' then
			
			--1.Pipeline adımı
			--Exponent'den biasın çıkarılması ve özel durum kontrolü
			----------------------------------------------		
			--Sign, exponent ve mantissa bitleri pipeline'a aktarılır
			s1 <= F1_Sign;
			e1 <= F1_Exponent - Bias;		
			m1(Mantissa - 1 downto 0) <= F1_Mantissa;
			
			--Exponent denormalize ise leading biti resetlenir
			if F1_Exponent = DenormalizeExponent then
				m1(Mantissa) <= '0';
			--Değil ise setlenir
			else
				m1(Mantissa) <= '1';
			end if;
			
			--Aynı şeyleri 2.sayı içinde yap
			s2 <= F2_Sign;
			e2 <= F2_Exponent - Bias;		
			m2(Mantissa - 1 downto 0) <= F2_Mantissa;
			
			if F2_Exponent = DenormalizeExponent then
				m2(Mantissa) <= '0';
			else
				m2(Mantissa) <= '1';
			end if;
			
			--Özel değer kontrolü
			--Eğer sayılardan ez az biri özel sayı(Inf, Nan) ise
			if F1_Exponent = SpecialExpoent or F2_Exponent = SpecialExpoent then
				--İkisinden en az biri NaN ise sonuç NaN
				if (IsNaN(F1) or IsNaN(F2)) = '1' then
					Exception <= NotaNumber;
				--İkiside Inf ise sonuç NaN
				elsif (IsInf(F1) and IsInf(F2)) = '1' then
					Exception <= NotaNumber;
				--İkisinden en az biri Inf ise
				elsif (IsInf(F1) or IsInf(F2)) = '1' then
						--Diğer sayı da 0 ise sonuç NaN
						if (IsZero(F1) or IsZero(F2)) = '1' then
							Exception <= NotaNumber;
						--0 değil ise sonuç Inf
						else
							Exception <= Infinity;
						end if;
				end if;
			--Sayılardan hiç biri özel değil ise sonuç normal
			else
				Exception <= NoException;
			end if;	
			----------------------------------------------
			
			--2.Pipeline adımı
			--Sign bitinin hesaplanması, exponentlerin toplanması ve
			--mantissaların çarpılması
			----------------------------------------------
			--Sign biti hesaplanır
			s1s2 <= s1 xor s2;
			
			--Exponentler toplanır
			e1e2 <= e1 + e2;
			
			--Exponentlerin toplamında taşma var ise sonuç Inf
			if signed(e1) > signed(Bias) and signed(e2) > signed(Bias) then
				if Exception = NoException then
					Exception_2 <= Infinity;
				else
					Exception_2 <= Exception;
				end if;
			--Yok ise Exception'u pipeline'ın bir sonraki adımına gönder
			else
				Exception_2 <= Exception;
			end if;
			
			--Mantissa'lar çarpılır
			m1m2Signal := m1 * m2;
			
			--Çarpımın değerli kısmı alınır
			m1m2 <= m1m2Signal(Mantissa * 2 + 1 downto Mantissa + 1);
			
			--Round ve Sticky bitleri alınır
			RoundBit <= m1m2Signal(Mantissa - 1);
			StickyBit <= m1m2Signal(Mantissa - 2);
			----------------------------------------------
			
			--3.Pipeline adımı
			--Prenormalization ve yuvarlama
			----------------------------------------------
			--Sign biti pipeline'ın bir sonraki adımına gönderilir
			s1s2_2 <= s1s2;
			
			if m1m2(Mantissa) = '1' then
				e1e2_2 <= e1e2 + 1;
				
				--Exponent'de taşma var ise sonuç Inf
				if signed(e1e2) > signed(Bias) then
					if Exception_2 = NoException then
						Exception_3 <= Infinity;
					else
						Exception_3 <= Exception_2;
					end if;
				else
					Exception_3 <= Exception_2;
				end if;
				
			else
			
				e1e2_2 <= e1e2;			
				Exception_3 <= Exception_2;
				
			end if;
				
			--Sıfıra yuvarla
			if RoundingMode = RoundtoZero then
			
				--Round ve Sticky bitleri kırpılarak sayı 0'a yaklaştırılır
				Rounded_m1m2 := m1m2;
			
			--En yakın çift sayıyı yuvarla
			elsif RoundingMode = RoundtoNearestEven then
			
				--Sayı xx.5 ya da xx.5'den büyük ise
				if RoundBit = '1' then
					--Sayı xx.75'den büyük ise 1 arttırılır
					if StickyBit = '1' then
						Rounded_m1m2 := m1m2 + 1;
					--Sayı xx.5 ise en yakın çift sayıya yuvarlanır
					else
						--Sayı tek ise 1 arttırarak çift sayıya yuvarlanır
						if m1m2(0) = '1' then
							Rounded_m1m2 := m1m2 + 1;
						--Sayı zaten çift ise olduğu gibi kalır
						else
							Rounded_m1m2 := m1m2;
						end if;
					end if;
				--Sayı xx.5'den küçük ise olduğu gibi kalır
				else
					Rounded_m1m2 := m1m2;
				end if;
			
			--+Sonsuza yuvarla
			elsif RoundingMode = RoundtoPlusInfinity then
			
				--Sayı xx.0'dan büyük ise
				if (RoundBit or StickyBit) = '1' then
					--Sayı pozitif ise 1 arttır
					if s1s2 = '0' then
						Rounded_m1m2 := m1m2 + 1;
					--Değil ise olduğu gibi bırak
					else
						Rounded_m1m2 := m1m2;
					end if;
				--Sayı xx.0 ise olduğu gibi bırak
				else
					Rounded_m1m2 := m1m2;
				end if;

			---Sonsuza yuvarla
			elsif RoundingMode = RoundtoMinusInfinity then
			
				--Sayı xx.0'dan büyük ise
				if (RoundBit or StickyBit) = '1' then
					--Sayı negatif ise 1 arttır
					if s1s2 = '1' then
						Rounded_m1m2 := m1m2 + 1;
					--Değil ise olduğu gibi bırak
					else
						Rounded_m1m2 := m1m2;
					end if;
				--Sayı xx.0 ise olduğu gibi bırak
				else
					Rounded_m1m2 := m1m2;
				end if;
			
			end if;
			
			--Leading biti resetlenir
			Rounded_m1m2(Mantissa) := '0';
			
			m1m2_2 <= Rounded_m1m2;	
			----------------------------------------------
			
			--4.Pipeline adımı
			--Postnormalization
			----------------------------------------------
			s3 <= s1s2_2;
			
			if m1m2_2(Mantissa) = '1' then
				e3 <= e1e2_2 + 1;
				
				--Exponent taşma kontrolü
				if signed(e1e2_2) > signed(Bias) then
					if Exception_3 = NoException then
						Exception_4 <= Infinity;
					else
						Exception_4 <= Exception_3;
					end if;
				else
					Exception_4 <= Exception_3;
				end if;
				
			else
			
				e3 <= e1e2_2;	
				Exception_4 <= Exception_3;
				
			end if;
			
			m3 <= m1m2_2;
			----------------------------------------------
			
			--5.Pipeline adımı
			--Exponent'e bias'ın eklenmesi ve sonuçların
			--çıkışa aktarılması
			----------------------------------------------
			if Exception_4 = NoException then
				F3_Exponent <= e3 + Bias;
				F3_Mantissa <= m3(Mantissa - 1 downto 0);
			--Sonsuz
			elsif Exception_4 = Infinity then
				F3_Exponent <= SpecialExpoent;
				F3_Mantissa <= ZerosMantissa;
			--NaN
			elsif Exception_4 = NotaNumber then
				F3_Exponent <= SpecialExpoent;
				F3_Mantissa <= OnesMantissa;
			end if;
			
			F3_Sign <= s3;
			
			Exception_Inf <= Exception_4(0);
			Exception_NaN <= Exception_4(1);
			----------------------------------------------
					
		end if;	
			
	end process;

end Behavioral;

Quartus II tarafından oluşturulan RTL şeması:

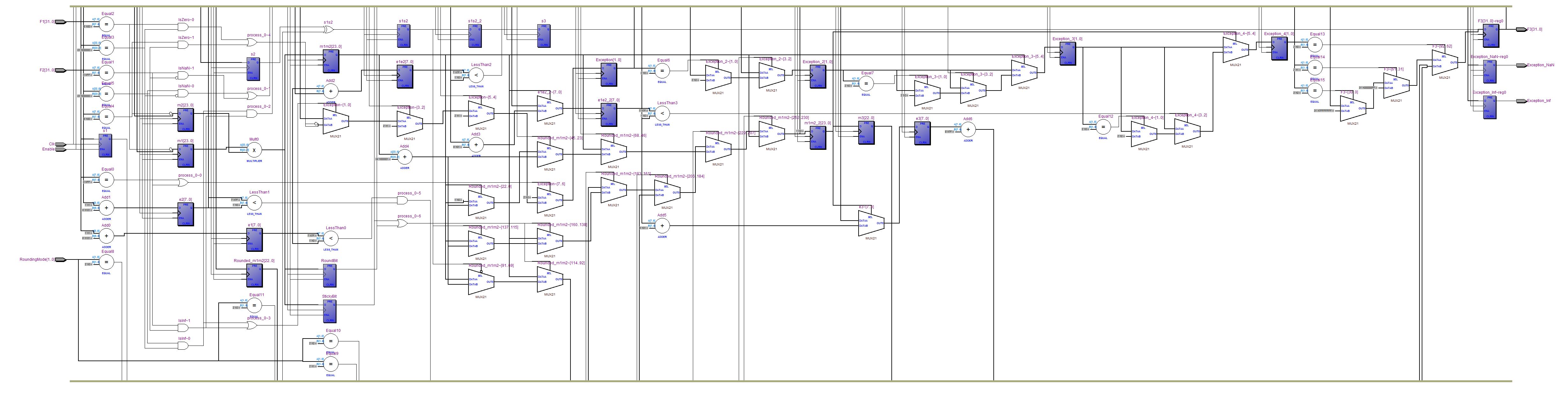Single precision için kaynak kullanımı: