olsun.
olsun.  ,
,  ve
ve  olmak üzere:
olmak üzere:

yazılabilir.  değerini tüm reel sayılarda genelleştirmek için faktöriyel yerine gama fonksiyonunu kullanalım. Gama fonksiyonu:
değerini tüm reel sayılarda genelleştirmek için faktöriyel yerine gama fonksiyonunu kullanalım. Gama fonksiyonu:

şeklinde verilir.  için genelleştirilmiş türevi gama fonksiyonu kullanarak şu şekilde yazabiliriz:
için genelleştirilmiş türevi gama fonksiyonu kullanarak şu şekilde yazabiliriz:

 fonksiyonun yarım (
fonksiyonun yarım ( ) türevini bulmak için,
) türevini bulmak için,  yerine
yerine  koyarsak:
koyarsak:

elde ederiz.
 içinde türevi hesaplarsak:
içinde türevi hesaplarsak:


 olduğuna göre:
olduğuna göre:

elde ederiz.
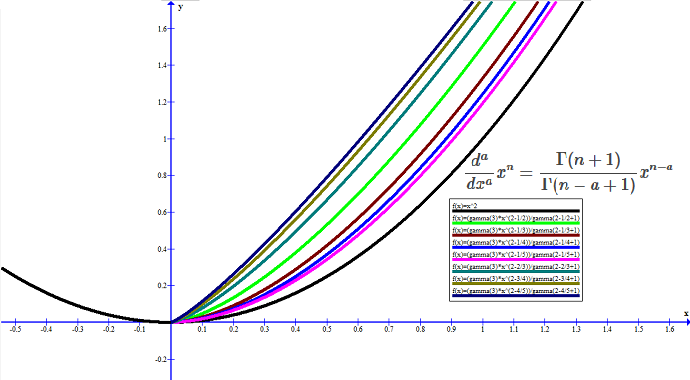
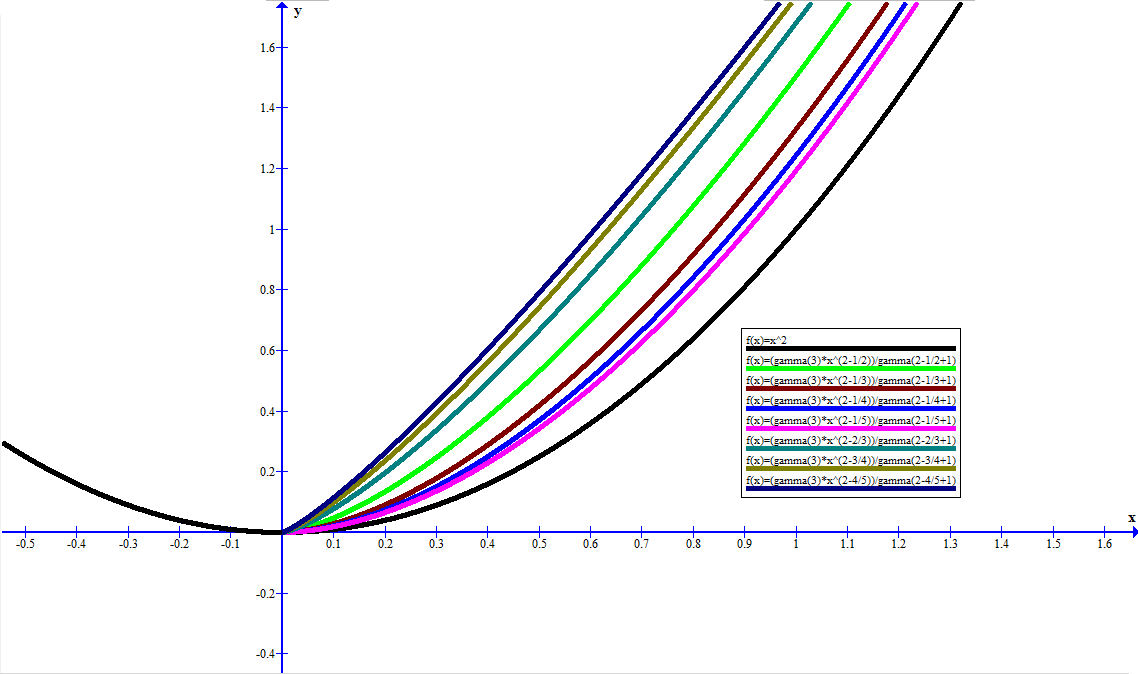
 fonksiyonunun farklı türevlerinin grafiği:
fonksiyonunun farklı türevlerinin grafiği: