f(x)=xn olsun. n∈Z+, n≥a ve a∈Z olmak üzere:
dadxaxn=n!(n−a)!xn−a
yazılabilir. a değerini tüm reel sayılarda genelleştirmek için faktöriyel yerine gama fonksiyonunu kullanalım. Gama fonksiyonu:
Γ(z)=(z−1)!=∫∞0xz−1e−xdx
şeklinde verilir. f(x) için genelleştirilmiş türevi gama fonksiyonu kullanarak şu şekilde yazabiliriz:
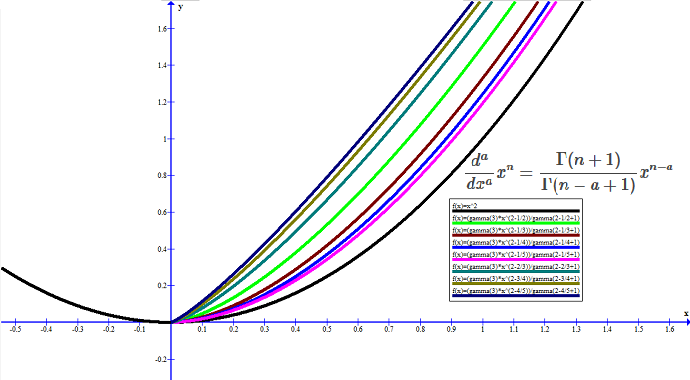
dadxaxn=Γ(n+1)Γ(n−a+1)xn−aa∈R,n≥a
f(x) fonksiyonun yarım (12.) türevini bulmak için, a yerine 12 koyarsak:
d12dx12xn=Γ(n+1)Γ(n+12)xn−12
elde ederiz.
n=2 içinde türevi hesaplarsak:
d12dx12x2=Γ(3)Γ(2+12)x32
d12dx12x2=2x32(32)(12)Γ(12)
Γ(12)=√π olduğuna göre:
d12dx12x2=8x3√xπ
elde ederiz.
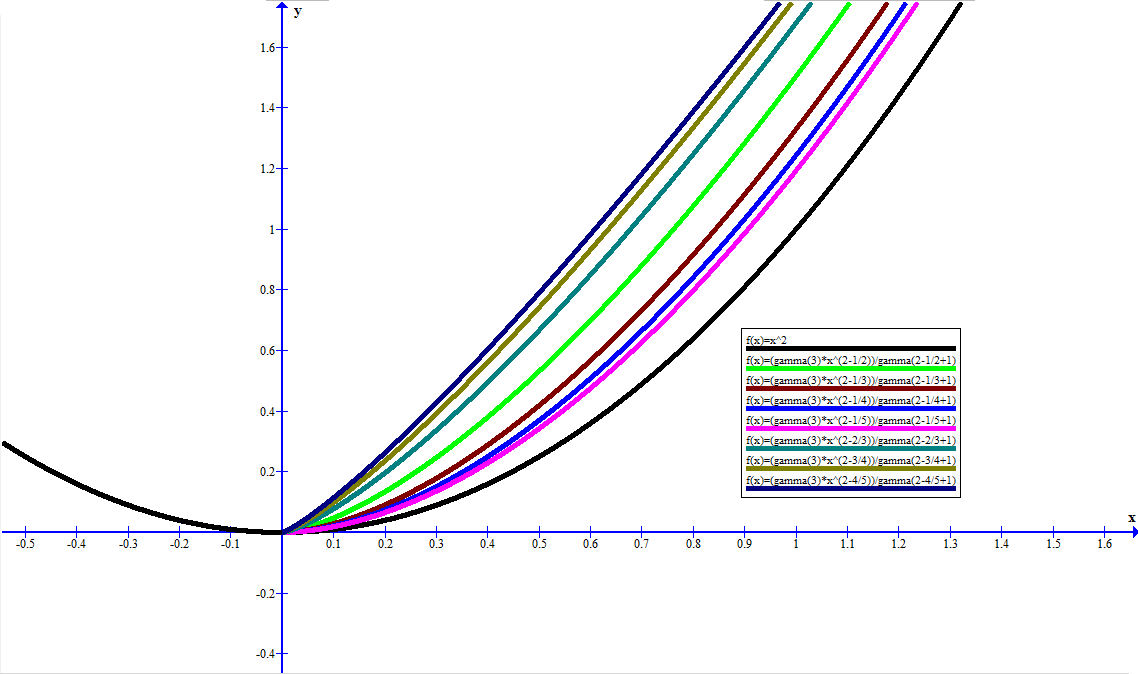
f(x)=x2 fonksiyonunun farklı türevlerinin grafiği: