Stm32f4 – 3D Kütüphanesi #1 (Tel-Kafes Modeli, Dönüşüm Matrisi)

Noktalar ve bu noktaları birleştiren çizgilerden oluşan modelleme sistemi Tel-Kafes Modelleme olarak adlandırılır. Diğer modelleme sistemlerinden daha basit ve kullanışsızdır ama diğer modelleme sistemlerinin de temelini oluşturur. Aşağıda tel-kafes ile modellenen Utah Teapot görülmektedir.

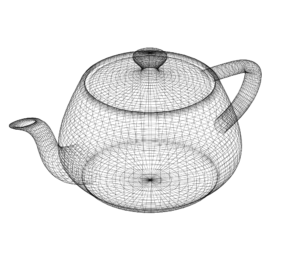
Bu yazımda basit ve kısa bir şekilde tel-kafes modelinin C diline aktarılmasını, dönüşüm matrisi ile eksenler etrafında nasıl dönüşüm yapılacağını ve bunların Stm32f4 kiti üzerinde gösterimini yapacağım.

Modelin tanımlanması

Bir objenin tel-kafes modelini struct ile şu şekilde tanımlayabiliriz:

typedef struct {
    //Kullanılan nokta ve cizgi sayisi   
    uint16_t NoktaSayisi;
    uint16_t CizgiSayisi;

    //Noktaların koordinatları(x,y,z)
    float (*Noktalar)[3];

    //Hangi noktaların birbiri ile birleşecegini
    //belirten dizi(nokta0,nokta1)
    uint16_t (*Cizgiler)[2];
 
    //Objenin koordinatı(x,y,z)
    float Koordinat[3];
  
    //Objenin merkez koordinatı(x,y,z)
    float Merkez[3];
   
    //Objenin cizgilerinin rengi(RGB565)
    uint16_t Renk;
}GL_Obje;

NoktaSayisi ve CizgiSayisi, objede kullanılan toplam nokta ve cizgi sayisi hakkinda bilgi verir. Bu sayilar modeli çizerken ve döndürürken işimize yarayacaktır. uint16_t şeklinde tanımlandığından dolayı en fazla $2^{16}$ tane nokta ve çizgi tanımlayabiliriz. Noktalar 3 elemanlı bir dizi olup her elemanında noktanın koordinatlarını içeren değerler bulunur. Çizgiler 2 elemanlı bir dizi olup, hangi noktanın hangi nokta ile birleşeceğini gösterir. Örneğin cizgi[0] = {0, 1} şeklinde bir tanımlama varsa bu nokta[0]'dan nokta[1]'e bir çizgi olduğu anlamına gelir. Koordinat ve Merkez de 3 elemanlı bir dizi olup objenin koordinatı ve merkezini gösterir. Bu değerler obje döndürülürken ve yeniden boyutlandırılırken kullanılabilir. Son olarak Renk de çizgilerin rengini belirtir. Obje çizilirken bu değer kullanılır.

Modelin Çizilmesi

Bütün çizgileri aşağıdaki fonksiyon ile çizdirebiliriz.

//Ekrana (x0, y0) noktasindan (x1, y1) noktasina
//Renk renginde cizgi cizen fonksiyon
void GL_2DCizgiCiz(x0, y0, x1, y1, Renk);

/** @Tanim : Obje'yi ekrana cizgiler yardimi(Tel-Kafes) ile cizen fonksiyon
  * @Parametreler : Obje = Cizilecek objenin adresi
  */
void GL_3DObjeCiz(GL_Obje *Obje)
{
  //Toplam cizgi sayisi kadar dongude kal
  for(int i = 0; i < Obje->CizgiSayisi; i++) 
      //Cizgiler dizisinin indeksledigi noktaları birbiri ile birleştir
      GL_2DCizgiCiz(Obje->Noktalar[Obje->Cizgiler[i][0]][0], //nokta0(x)
      Obje->Noktalar[Obje->Cizgiler[i][0]][1], //nokta0(y)
      Obje->Noktalar[Obje->Cizgiler[i][1]][0], //nokta1(x)
      Obje->Noktalar[Obje->Cizgiler[i][1]][1], //nokta1(y)
      Obje->Renk); //renk(RGB565)
}

Küp Modeli

Birim kübü el ile aşağıdaki şekilde tanımlayabiliriz.

//Noktaların koordinatlari
float Kup_Noktalar[8][3] = {
  0, 0, 0,
  1, 0, 0,
  1, 0, 1,
  0, 0, 1,
  0, 1, 0,
  1, 1, 0,
  1, 1, 1,
  0, 1, 1 };

//Hangi noktalarin birbiri ile birleşeceğini
//gösteren dizi
uint16_t Kup_Cizgiler[12][2] = {
  0,1,
  1,2,
  2,3,
  3,0,
  4,5,
  5,6,
  6,7,
  7,4,
  0,4,
  1,5,
  2,6,
  3,7 };

//Kup objesi yarat
GL_Obje Kup;

//Onceden belirlenmis degerleri bu objeye at
Kup.NoktaSayisi = 8;
Kup.CizgiSayisi = 12;
Kup.Noktalar = Kup_Noktalar;
Kup.Cizgiler = Kup_Cizgiler;
Kup.Merkez[0] = 0.5;
Kup.Merkez[1] = 0.5;
Kup.Merkez[2] = 0.5;
Kup.Koordinat[0] = 0;
Kup.Koordinat[1] = 0;
Kup.Koordinat[2] = 0;
Kup.Renk = 0xFFFF; //Beyaz

Her obje için tek tek koordinatları ve çizgileri hesaplamak çok zaman alacağından bu işi bir fonksiyon ile yapabiliriz.

/** @Tanım : Istenen buyuklukte, koordinatta ve renkte kup yaratan fonksiyon
  * @Parametreler : Kup = yaratilmak istenen Objenin adresi,
  *                 x, y, z = Objenin koordinatlari
  *                 Uzunluk = Kupun bir kenarinin uzunlugu
  *                 Renk = Objenin cizgilerinin rengi
  */ 
void GL_3DKupYarat(GL_Obje* Kup, float x, float y, float z, float Uzunluk, uint16_t Renk)
{        
    //Kupun noktalarinin tanimlanmasi
    float Kup_Noktalari[8][3] = {
        x,           y,            z,
        x + Uzunluk, y,            z,
        x + Uzunluk, y,            z + Uzunluk,
        x,           y,            z + Uzunluk,
        x,           y + Uzunluk,  z,
        x + Uzunluk, y + Uzunluk,  z,
        x + Uzunluk, y + Uzunluk,  z + Uzunluk,
        x,           y + Uzunluk,  z + Uzunluk };
    
    //Kupun cizgilerinin tanimlanamasi
    uint16_t Kup_Cizgileri[12][2] = {
        0, 1,
        1, 2,
        2, 3,
        3, 0,    
        4, 5,
        5, 6,
        6, 7,
        7, 4,        
        0, 4,
        1, 5,
        2, 6,
        3, 7
    };
    
    //Dinamik bellekte yer ayrilmasi ve bu ayrilan yere
    //önceden tanimlanmis noktalarin ve cizgilerin kopyalanmasi    
    float *_Kup_Noktalari = (float *)malloc(sizeof(Kup_Noktalari));
    memcpy(_Kup_Noktalari, Kup_Noktalari, sizeof(Kup_Noktalari));
    
    uint16_t *_Kup_Cizgileri = (uint16_t *)malloc(sizeof(Kup_Cizgileri));
    memcpy(_Kup_Cizgileri, Kup_Cizgileri, sizeof(Kup_Cizgileri));
    
    //Tanimlanmis özelliklerin Kup objesine aktarilmasi
    Kup->NoktaSayisi = 8;
    Kup->CizgiSayisi = 12;
    Kup->Noktalar = (float (*)[3])_Kup_Noktalari;
    Kup->Cizgiler = (uint16_t (*)[2])_Kup_Cizgileri;
    Kup->Koordinat[0] = x;
    Kup->Koordinat[1] = y;
    Kup->Koordinat[2] = z;
    Kup->Merkez[0] = x + Uzunluk / 2;
    Kup->Merkez[1] = y + Uzunluk / 2;
    Kup->Merkez[2] = z + Uzunluk / 2;
    Kup->Renk = Renk;
}

Objenin bir eksen etrafında döndürülmesi

Dönüşüm matrisi bir noktayı belli bir eksen etrafında döndüren matrise verilen isimdir. $(X,Y,Z)$ düzleminde bir noktayı $X$ ekseni etrafında döndüren matris aşağıdaki gibidir.

$R_{x}(\theta) = \begin{bmatrix}1&0&0\\0&\cos(\theta)&-\sin(\theta)\\0&\sin(\theta)&\cos(\theta)\end{bmatrix}$

Benzer şekilde $Y$ ve $Z$ ekseni etrafında döndüren matrisler :

$R_{y}(\theta) = \begin{bmatrix}\cos(\theta)&0&\sin(\theta)\\0&1&0\\-\sin(\theta)&0&\cos(\theta)\end{bmatrix}$

$R_{z}(\theta) = \begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix}$

Bir noktayı hem $X$ hem $Y$ hem de $Z$ ekseni etrafında döndürmek için bu 3 matrisin çarpılması gerekir.

$\small{R_{x}(\alpha)R_{y}(\beta)R_{z}(\gamma)=\\\begin{bmatrix}\cos(\beta)\cos(\gamma)&\cos(\gamma)\sin(\alpha)\sin(\beta)-\cos(\alpha)sin(\gamma)&\cos(\alpha)\cos(\gamma)\sin(\beta)+sin(\alpha)\sin(\gamma)\\\cos(\beta)\sin(\gamma)&\cos(\alpha)\cos(\gamma)+\sin(\alpha)\sin(\beta)\sin(\gamma)&-\cos(\gamma)\sin(\alpha)+cos(\alpha)\sin(\beta)\sin(\gamma)\\-\sin(\beta)&\cos(\beta)\sin(\alpha)&\cos(\alpha)\cos(\beta)\end{bmatrix}}$

Matrisler yukarıdaki sıra ile çarpıldığında, ilk olarak $X$ sonra $Y$ ve en son $Z$ ekseni etrafında dönüşüm yapılır.

Bu dönüşüm matrisini fonksiyona dönüştürürsek:

/** @Tanim : Objeyi belirlenen nokta etrafinda belirlenen acida döndüren fonksiyon
  * @Parametreler : Obje = Donusume ugrayacak obje
  *                 DonusumMerkezi = Donusumun yapilacagi referans(merkez) noktasi,
  *                 eğer tanimlanmamis(NULL) ise Obje'de tanimlanan merkez noktasi
  *                 Donunum_x, Donunum_y, Donunum_z = Derece cinsinden donusum acisi
  */
void GL_3DDonusum(GL_Obje *Obje, float *DonusumMerkezi, float Donusum_x, float Donusum_y, float Donusum_z)
{
    //Derecenin radyana donusturulmesı
    float Aci_x = Donusum_y * PI / 180;
    float Aci_y = Donusum_x * PI / 180;
    float Aci_z = Donusum_z * PI / 180;
    
    //Donusum matrisine girecek noktalar
    float Cor_x, Cor_y, Cor_z;
    
    //Butun noktalar icin dongude kal
    for(int i = 0; i < Obje->NoktaSayisi; i++){
        
        //Donusum matrisine girecek noktalari bul
        
        //Belirlenen noktada donusum yapabilmek icin referans koordinatini, 
        //objenin nokta koordinatindan cikar
        //(Donunsum merkezini, (x, y, z) = (0, 0, 0) noktasina otele)
        if(Donusummerkezi != NULL){        
            Cor_x = Obje->Noktalar[i][0] - DonusumMerkezi[0];
            Cor_y = Obje->Noktalar[i][1] - DonusumMerkezi[1];
            Cor_z = Obje->Noktalar[i][2] - DonusumMerkezi[2];}
        else{
            //DonusumMerkezi tanimlanmamis(NULL) ise objenin merkezi etrafında donusum yap
            Cor_x = Obje->Noktalar[i][0] - Obje->Merkez[0];
            Cor_y = Obje->Noktalar[i][1] - Obje->Merkez[1];
            Cor_z = Obje->Noktalar[i][2] - Obje->Merkez[2];
        }
        
        //Noktalari donusum matrisi ile carp

        #ifndef ARM_MATH_CM4
        Obje->Noktalar[i][0] = cos(Aci_x) * cos(Aci_z) * Cor_x + (cos(Aci_z) * sin(Aci_y) * sin(Aci_x) - cos(Aci_y) * sin(Aci_z)) * Cor_y + (cos(Aci_y) * cos(Aci_z) * sin(Aci_x) + sin(Aci_y) * sin(Aci_z)) * Cor_z;
        Obje->Noktalar[i][1] = cos(Aci_x) * sin(Aci_z) * Cor_x + (cos(Aci_y) * cos(Aci_z) + sin(Aci_y) * sin(Aci_x) * sin(Aci_z)) * Cor_y + (-cos(Aci_z) * sin(Aci_y) + cos(Aci_y) * sin(Aci_x) * sin(Aci_z)) * Cor_z;
        Obje->Noktalar[i][2] = -sin(Aci_x) * Cor_x + cos(Aci_x) * sin(Aci_y) * Cor_y + cos(Aci_y) * cos(Aci_x) * Cor_z;
        
        //CM4 DSP icin daha hizli fonksiyonlar
        #else
        Obje->Noktalar[i][0] = arm_cos_f32(Aci_x) * arm_cos_f32(Aci_z) * Cor_x + (arm_cos_f32(Aci_z) * arm_sin_f32(Aci_y) * arm_sin_f32(Aci_x) - arm_cos_f32(Aci_y) * arm_sin_f32(Aci_z)) * Cor_y + (arm_cos_f32(Aci_y) * arm_cos_f32(Aci_z) * arm_sin_f32(Aci_x) + arm_sin_f32(Aci_y) * arm_sin_f32(Aci_z)) * Cor_z;
        Obje->Noktalar[i][1] = arm_cos_f32(Aci_x) * arm_sin_f32(Aci_z) * Cor_x + (arm_cos_f32(Aci_y) * arm_cos_f32(Aci_z) + arm_sin_f32(Aci_y) * arm_sin_f32(Aci_x) * arm_sin_f32(Aci_z)) * Cor_y + (-arm_cos_f32(Aci_z) * arm_sin_f32(Aci_y) + arm_cos_f32(Aci_y) * arm_sin_f32(Aci_x) * arm_sin_f32(Aci_z)) * Cor_z;
        Obje->Noktalar[i][2] = -arm_sin_f32(Aci_x) * Cor_x + arm_cos_f32(Aci_x) * arm_sin_f32(Aci_y) * Cor_y + arm_cos_f32(Aci_y) * arm_cos_f32(Aci_x) * Cor_z;        
        #endif //ARM_MATH_CM4
        
        //Cikarilan degerleri tekrar topla
        if(Donusummerkezi != NULL){
            Obje->Noktalar[i][0] += DonusumMerkezi[0];
            Obje->Noktalar[i][1] += DonusumMerkezi[1];
            Obje->Noktalar[i][2] += DonusumMerkezi[2];}
        else{
            Obje->Noktalar[i][0] += Obje->Merkez[0];
            Obje->Noktalar[i][1] += Obje->Merkez[1];
            Obje->Noktalar[i][2] += Obje->Merkez[2];
        }
    }
}

Stm32f4 Kitinde Örnek Uygulama

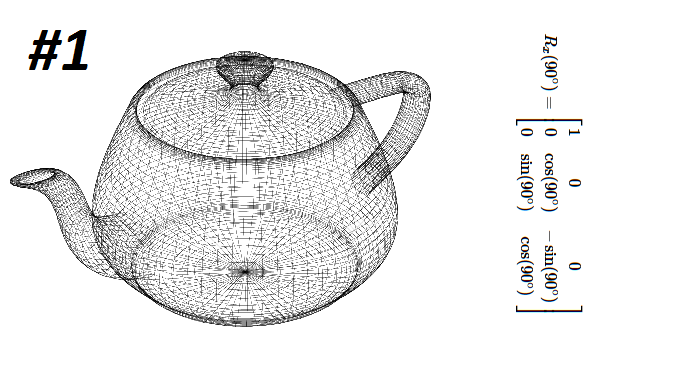
Bu uygulamada bir kenarı 100 birim olan küpü her 30ms de kendi merkezinde, bütün eksenler etrafında 2 derece döndürdük ve bunu kitin ekranında gösterdik.

#include "stm32f4xx.h"
#include "donanim.h"
#include "3D.h"

#define BEYAZ 0xFFFF

int main()
{
    //GPIO, LTDC, FMC... donanimlarini aktif et
    DonanimiHazirla();
    
    //Kup objesini olustur
    GL_Obje Kup;
    
    //Kup objesini gercek bir kup objesine donustur
    GL_3DKupYarat(&Kup, 100, 60, 0, 120, BEYAZ);
    
    while(1){
        //Ekrani temizle
        GL_EkraniTemizle();
        
        //Kup objesini ciz
        GL_3DObjeCiz(&Kup);
        
        //Kup objesini kendi merkezinde butun eksenler etrafinda 2 derece dondur
        GL_3DDonusum(&Kup, NULL, 2, 2, 2);
        
        //30ms bekle ve basa don
        Bekle(30);
    }
        
}

Video :

3 thoughts on “Stm32f4 - 3D Kütüphanesi #1 (Tel-Kafes Modeli, Dönüşüm Matrisi)”

Aldo Vargas dedi ki:

11 Aralık 2016, 10:00 PM

Hello!
Its very impressive the word and how you manage the display. Do you think I can get the project for a school work? I need to do preety much the same but with a sphere, so far I printed one in a 2d reference but this kind of modeling gets me in trouble. Thanks!

https://www.dropbox.com/s/3rzrbsppk0h3pp4/IMG_20161211_155536.jpg?dl=0

Cevapla
1. Bertan Taşkın dedi ki:
  
  12 Aralık 2016, 11:49 AM
  
  Hey, thanks for your comment, can you reach me via iletisim@bertantaskin.com and we can discuss details.
  
  Cevapla
Emre İRİŞ dedi ki:

18 Aralık 2019, 3:10 PM

Valla tebrik ederim. Çok güzel işler yapmışsın helal olsun.

Cevapla