CORDIC yani COordinate Rotation DIgital Computer, bilgisayarlarda kullanılan ve trigonometrik fonksiyonları kısa yoldan en az hata ile hesaplamada kullanılan bir algoritmadır. Algoritmanın temeli, bir noktanın orjin etrafında gitgide azalan bir açı ile döndürülmesinden gelir.  , dönüşüm matrisi olmak üzere yapılan işlemleri matematiksel olarak şu şekilde yazabiliriz:
, dönüşüm matrisi olmak üzere yapılan işlemleri matematiksel olarak şu şekilde yazabiliriz:


Dönüşüm matrisindeki  ve
ve  ifadelerini
ifadelerini  cinsinden yazalım.
cinsinden yazalım.



Elimizde  olmak üzere
olmak üzere  ve
ve  değerlerinden oluşan tablolarımız olsun. Bu tabloları kullanarak istediğimiz değerdeki
değerlerinden oluşan tablolarımız olsun. Bu tabloları kullanarak istediğimiz değerdeki  ve
ve  değerlerini bulabiliriz.
değerlerini bulabiliriz.





Burada  dönmenin yönünü belirtir.
dönmenin yönünü belirtir.  ya da
ya da  değerlerinden birini alabilir. Bu işlemler ne kadar tekrar edilirse istenilen
değerlerinden birini alabilir. Bu işlemler ne kadar tekrar edilirse istenilen  ve
ve  değerlerine o kadar yaklaşılır.
değerlerine o kadar yaklaşılır.
Bilgisayarlarda çarpma işlemi yapmak, kaydırma işlemi yapmaktan daha fazla zaman harcar. Bu yüzden  yerine işlemleri daha kolay hesaplanabilecek hale getiren
yerine işlemleri daha kolay hesaplanabilecek hale getiren  ifadesini yazalım ve
ifadesini yazalım ve  değerlerini bir tabloda saklayalım.
değerlerini bir tabloda saklayalım.





Her işlemde  değerini tekrar tekrar çarpmak yerine en son belirli iterasyon değeri için hesaplanmış
değerini tekrar tekrar çarpmak yerine en son belirli iterasyon değeri için hesaplanmış  ile çarparak işlemleri bitirebiliriz.
ile çarparak işlemleri bitirebiliriz.
 değeri için
değeri için  ve
ve  fonksiyonlarını
fonksiyonlarını  iterasyonda hesaplamaya çalışalım.
iterasyonda hesaplamaya çalışalım.







































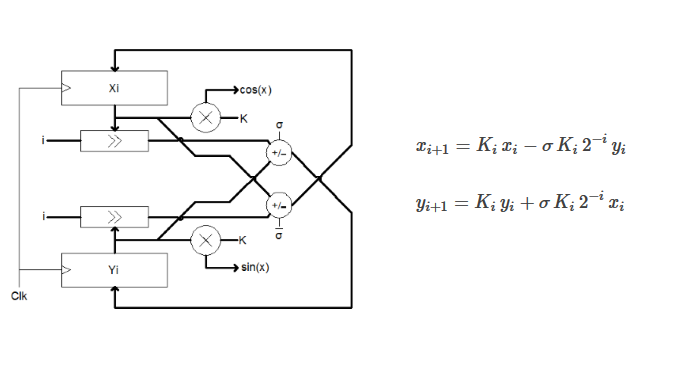
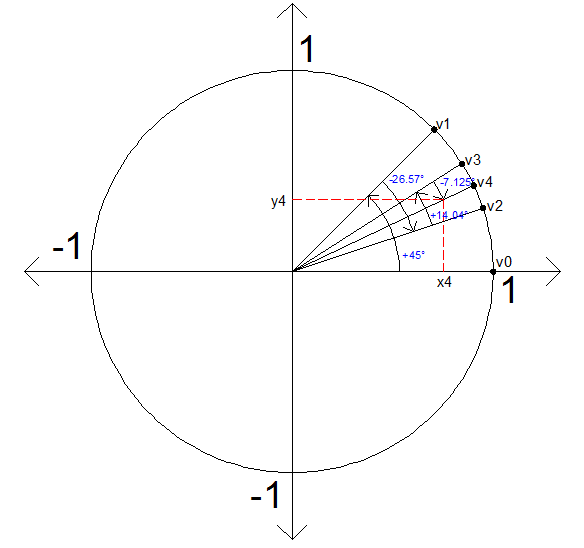
Burada  hesaplanan gerçek açıdır. Yaptığımız işlemler koordinat sisteminde aşağıdaki gibi olacaktır:
hesaplanan gerçek açıdır. Yaptığımız işlemler koordinat sisteminde aşağıdaki gibi olacaktır:
Kullanılacak sayı formatı  ve
ve  için
için  , açı için
, açı için  olarak seçilmiştir. Donanımın tasarımı aşağıdaki gibi olacaktır:
olarak seçilmiştir. Donanımın tasarımı aşağıdaki gibi olacaktır:
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
entity CORDIC is
port(Clk, Reset, S : in std_logic; --Clock, Reset ve S girişleri
Angle : in std_logic_vector(15 downto 0); --Hesaplanacak yeni açı girişi
Sin, Cos : out std_logic_vector(15 downto 0)); --Sin, Cos çıkışları
end CORDIC;
architecture Behavioral of CORDIC is
--Shifter
component ArithmeticShifter
port(DataIn : in std_logic_vector(15 downto 0);
i : in std_logic_vector(3 downto 0);
DataOut : out std_logic_vector(15 downto 0));
end component;
--Toplayıcı-Çıkarıcı
component Adder
generic(W : integer := 8);
port(Sigma : in std_logic;
A, B : in std_logic_vector(W - 1 downto 0);
O : out std_logic_vector(W - 1 downto 0));
end component;
--Çarpıcı(Q15 x Q15 = Q30)
component Multiplier
port(A, B : in std_logic_vector(15 downto 0);
O : out std_logic_vector(31 downto 0));
end component;
--Register
component Reg
generic(ResetValue : std_logic_vector(15 downto 0) := X"00");
port(Clk, Reset : in std_logic;
DataIn : in std_logic_vector(15 downto 0);
DataOut : out std_logic_vector(15 downto 0));
end component;
signal XiIn, XiOut : std_logic_vector(15 downto 0);
signal XiShifterOut : std_logic_vector(15 downto 0);
signal XiMultiplierOut : std_logic_vector(31 downto 0);
signal YiIn, YiOut : std_logic_vector(15 downto 0);
signal YiShifterOut : std_logic_vector(15 downto 0);
signal YiMultiplierOut : std_logic_vector(31 downto 0);
signal atanLUTOut : std_logic_vector(15 downto 0);
signal AngleOut, AngleIn : std_logic_vector(15 downto 0);
signal AngleAdderOut : std_logic_vector(15 downto 0);
signal Sigma : std_logic;
signal i : std_logic_vector(3 downto 0) := X"0";
signal CounterAdderOut : std_logic_vector(3 downto 0);
begin
--Xi Registeri
--Reset Değeri = 1 (UQ1.15)
Xi : Reg
generic map(X"8000")
port map(Clk, Reset, XiIn, XiOut);
--Xi için shifter
XShifter : ArithmeticShifter
port map(XiOut, i, XiShifterOut);
--Xi için Toplayıcı çıkarıcı
Adder1 : Adder
generic map(16)
port map(Sigma, YiOut, XiShifterOut, YiIn);
--Yi Registeri
--Reset Değeri = 0 (UQ1.15)
Yi : Reg
generic map(X"0000")
port map(Clk, Reset, YiIn, YiOut);
--Yi için shifter
YShifter : ArithmeticShifter
port map(YiOut, i, YiShifterOut);
--Yi için Toplayıcı çıkarıcı
Adder2 : Adder
generic map(16)
port map(not Sigma, XiOut, YiShifterOut, XiIn);
--Xi ve Yi'yi K katsayısı ile çarp
XiMultiplier : Multiplier
port map(XiOut, X"4DBA", XiMultiplierOut);
YiMultiplier : Multiplier
port map(YiOut, X"4DBA", YiMultiplierOut);
--Q30 -> Q15 için shift işlemi
Shift : for j in 0 to 15 generate
Sin(j) <= YiMultiplierOut(j + 15);
Cos(j) <= XiMultiplierOut(j + 15);
end generate;
--Açı Registeri
AngleRegister : Reg
generic map(X"0000")
port map(Clk, Reset, AngleIn, AngleOut);
AngleAdder : Adder
generic map(16)
port map(not Sigma, AngleOut, atanLUTOut, AngleAdderOut);
--Yeni açı girmek için multiplexer
with S select
AngleIn <= AngleAdderOut when '0',
Angle when others;
--Açının işaret bitini
Sigma <= AngleOut(15);
--Atan tablosu (Q1.14)
with i select
atanLUTOut <= X"3201" when X"0",
X"1DAC" when X"1",
X"0FAD" when X"2",
X"07F5" when X"3",
X"03FE" when X"4",
X"0200" when X"5",
X"0100" when X"6",
X"0080" when X"7",
X"0040" when X"8",
X"0020" when X"9",
X"0010" when X"A",
X"0008" when X"B",
X"0004" when X"C",
X"0002" when X"D",
X"0001" when X"E",
X"0000" when others;
--Counter
CounterAdder : Adder
generic map(4)
port map('0', i, X"1", CounterAdderOut);
process(Reset, Clk)
begin
if Reset = '1' then
i <= X"0";
elsif rising_edge(Clk) then
i <= CounterAdderOut;
end if;
end process;
end Behavioral;
Tasarımın diğer dosyalarına buradan ulaşabilirsiniz.