Polinom İnterpolasyonu

İnterpolasyon var olan değer kümesini kullanarak, bilinmeyen değerleri(ara değerleri) en az hata ile bulmamıza yarayan yöntemlerdir. Nümerik analizin bir konusu olup, mühendislikte de kullanılır. Linner, exponansiyel, kübik gibi türleri bulur. İnterpolasyon fonksiyonları ise bilinen değerler yardımı ile bu değerlere en az hata payı ile yaklaşan fonksiyonlardır. Fonksiyon linner, polinom, exponansiyel ya da özel bir türden olabilir. Bu yazıda değer kümesi belli olan bir kümenin en az hata payı ile bir polinoma aktarılmasını gösterilecektir.

Elimizde $x$ ve $y$ değerlerinden oluşan $m$ eleman sayisina sahip $\mathbf{X}=\{x_0,x_1,\dotsc,x_{m-1}\}$ ve $\mathbf{Y}=\{y_0,y_1,\dotsc,y_{m-1}\}$ kümelerimiz olsun.

$\begin{align*}\mathit{f}\;(\mathbf{X})=\mathbf{Y}+\mathit{E}\;(\mathbf{X})\end{align*}$ şeklinde tanımlanan $\mathit{f}$ fonksiyonunu, hata fonksiyonunu yani $\mathit{E}$ fonksiyonunu olabildiğince küçük tutarak bulmaya çalışalım.

$\mathit{f}$ fonksiyonumuz $n.$ dereceden bir polinom olduğundan $\mathit{f}$ fonksiyonunu şöyle yazabiliriz :

$\begin{align*}\mathit{f}\;(x)=A_{n}x^{n}+A_{n-1}x^{n-1}+A_{n-2}x^{n-2}+\dotsb+A_{0}=\sum^{n}_{p\,=\,0}A_px^p\end{align*}$

Burada $A_p$, fonksiyonumuzun katsayılarıdır. Fonksiyonu bulmak için bu değerleri bulmamız gerekir.

Hata fonksiyonunu yazalım:

$\mathit{E}(\mathbf{X})=\mathit{f}\;(\mathbf{X})-\mathbf{Y}$

Toplam hatayı şu şekilde yazabiliriz:

$\begin{align*}\mathit{E}=\sum^{m-1}_{k=0}\big(\mathit{f}\;(x_k)-y_k\big)^2\end{align*}$

Hata fonksiyonunu en az yapmak için, hata fonksiyonunun bütün $A$ katsayıları için türevinin $0$ olması gerekir. Herhangi bir $A_t$ için türev alıp $0$'a eşitlersek:

$\begin{align*}\frac{\partial\mathit{E}}{\partial{A_t}}=2\sum^{m-1}_{k=0}x^{t}_k\big(\mathit{f}\;(x_k)-y_k\big)\end{align*}$

$\begin{align*}\frac{\partial\mathit{E}}{\partial{A_t}}=0\to\sum^{m-1}_{k=0}\,x^{t}_k\mathit{f}\;(x_k)-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\mathit{f}$ fonksiyonunu açalım.

$\begin{align*}\sum^{m-1}_{k=0}\,\bigg[x^{t}_k\;\sum^{n}_{p=0}A_px^{p}_{k}\bigg]-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\begin{align*}\sum^{m-1}_{k=0}\,\bigg[x^{t}_k\;\big(A_{0}x^{0}_k+A_{1}x^{1}_k+A_{2}x^{2}_k+\dotsb+A_{n}x^{n}_k\big)\bigg]-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\begin{align*}\sum^{m-1}_{k=0}\,\big[A_{0}x^{t}_k+A_{1}x^{t+1}_k+A_{2}x^{t+2}_k+\dotsb+A_{n}x^{t+n}_k\big]-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\begin{align*}\sum^{m-1}_{k=0}\,A_{0}x^{t}_k+\sum^{m-1}_{k=0}\,A_{1}x^{t+1}_k+\sum^{m-1}_{k=0}\,A_{2}x^{t+2}_k+\dotsb+\sum^{m-1}_{k=0}\,A_{n}x^{t+n}_k-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\begin{align*}A_{0}\sum^{m-1}_{k=0}\,x^{t}_k+A_{1}\sum^{m-1}_{k=0}\,x^{t+1}_k+A_{2}\sum^{m-1}_{k=0}\,x^{t+2}_k+\dotsb+A_{n}\sum^{m-1}_{k=0}\,x^{t+n}_k-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

Soldaki toplam sembollü ifadelere $C$ diyelim.

$\begin{align*}A_{0}\underbrace{\sum^{m-1}_{k=0}\,x^{t}_k}_{C_t}+A_{1}\underbrace{\sum^{m-1}_{k=0}\,x^{t+1}_k}_{C_{t+1}}+A_{2}\underbrace{\sum^{m-1}_{k=0}\,x^{t+2}_k}_{C_{t+2}}+\dotsb+A_{n}\underbrace{\sum^{m-1}_{k=0}\,x^{t+n}_k}_{C_{t+n}}-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

$\begin{align*}A_0C_{t}+A_1C_{t+1}+A_2C_{t+2}+\dotsb+A_nC_{t+n}-\sum^{m-1}_{k=0}x^{t}_k\,y_k=0\end{align*}$

Sağdaki toplam sembollü ifadeye $P$ diyelim.

$\begin{align*}A_0C_{t}+A_1C_{t+1}+A_2C_{t+2}+\dotsb+A_nC_{t+n}-\underbrace{\sum^{m-1}_{k=0}x^{t}_k\,y_k}_{P_t}=0\end{align*}$

$\begin{align*}A_0C_{t}+A_1C_{t+1}+A_2C_{t+2}+\dotsb+A_nC_{t+n}-P_t=0\end{align*}$

$\begin{align*}A_0C_{t}+A_1C_{t+1}+A_2C_{t+2}+\dotsb+A_nC_{t+n}=P_t\end{align*}$

İfadenin başta $A_t$'ye göre türevini almıştık. Hata fonksiyonun en az olabilmesi için bütün $t$ değerleri($t$ en fazla $\mathit{f}$ fonksiyonunun derecesi olan $n$ olabilir) için türev almamız gerekir.

$A_0C_{0}+A_1C_{1}+A_2C_{2}+\dotsb+A_nC_{n}=P_0\\A_0C_{1}+A_1C_{2}+A_2C_{3}+\dotsb+A_nC_{n+1}=P_1\\A_0C_{2}+A_1C_{3}+A_2C_{4}+\dotsb+A_nC_{n+2}=P_2\\\vdots\\A_0C_{n}+A_1C_{n+1}+A_2C_{n+2}+\dotsb+A_nC_{2n}=P_n$

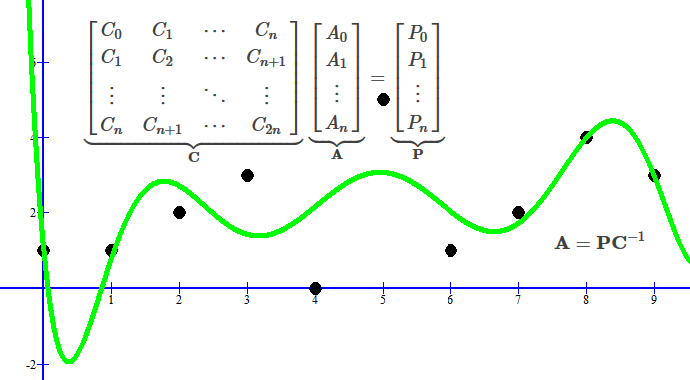
Bu denklemleride matris olarak yazarsak:

$\begin{align*}\underbrace{\begin{bmatrix}C_{0}&C_{1}&\cdots&C_{n}\\C_{1}&C_{2}&\cdots&C_{n+1}\\\vdots&\vdots&\ddots&\vdots\\C_{n}&C_{n+1}&\cdots&C_{2n}\end{bmatrix}}_{\mathbf{C}}\;\underbrace{\begin{bmatrix}A_0\\A_1\\\vdots\\A_n\end{bmatrix}}_{\mathbf{A}}=\underbrace{\begin{bmatrix}P_0\\P_1\\\vdots\\P_n\end{bmatrix}}_{\mathbf{P}}\end{align*}$

$\begin{align*}\mathbf{C}\mathbf{A}=\mathbf{P}\end{align*}$

Her iki tarafı $\mathbf{C}^{-1}$ ile çarparsak:

$\begin{align*}\mathbf{A}=\mathbf{P}\mathbf{C}^{-1}\end{align*}$

elde ederiz.