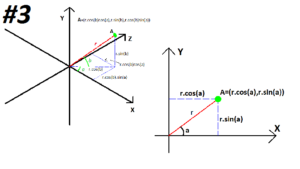
Bu yazımda küp dışındaki bazı geometrik cisimlerin tel-kafes yöntemi ile nasıl üretebileceğimizi göstereceğim. 1.Dikdörtgen Prizma Küpteki tek bir kenarının uzunluğu olan "Uzunluk" argümanı yerine "a, b, c" argümanları yazarak her Daha fazla...
Loop Unrolling, programlamada yapılabilecek optimizasyon türlerinde biridir. Adından da anlaşılabileceği gibi döngünün açılması(uzatılması)dır. Örnek vermek gerekirse, aşağıdaki gibi bir döngümüz olsun. Bu döngünün açılmış hali aşağıdaki gibidir: Döngülerin bu şekilde Daha fazla...
olsun. , ve olmak üzere: yazılabilir. değerini tüm reel sayılarda genelleştirmek için faktöriyel yerine gama fonksiyonunu kullanalım. Gama fonksiyonu: şeklinde verilir. için genelleştirilmiş türevi gama fonksiyonu kullanarak şu şekilde yazabiliriz: Daha fazla...
Bu yazımda obje üzerinde öteleme ve ölçeklendirme işlemlerini gösterip bu işlemlerin Stm32f4 kiti üzerinde uygulamasını yapacağım. Öteleme Öteleme bütün noktaların belli bir yönde ve uzunlukta yer değiştirmesidir. nokta ve öteleme Daha fazla...
İnterpolasyon var olan değer kümesini kullanarak, bilinmeyen değerleri(ara değerleri) en az hata ile bulmamıza yarayan yöntemlerdir. Nümerik analizin bir konusu olup, mühendislikte de kullanılır. Linner, exponansiyel, kübik gibi türleri bulur. Daha fazla...
